EdmondFrank's 时光足迹

この先は暗い夜道だけかもしれない　それでも信じて進むんだ。星がその道を少しでも照らしてくれるのを。
或许前路永夜，即便如此我也要前进，因为星光即使微弱也会我为照亮前途。
——《四月は君の嘘》

Apriori与关联分析

- -

关联分析

相关概念

作为经典的机器学习算法来说，关联分析并不算复杂。简单来说，从大规模数据集中寻找物品间的隐含关系被称作关联分析(association analysis)或者关联规则学习(association rule learning)。而其中关联分析的关键就是在众多的物品组成的项集(itemset)中找到那些经常一起出现的物品集合，也就是我们所谓的频繁项集。由于寻找物品的不同组合是一项非常耗时的任务，所需的计算代价也非常的高，这样显然用蛮力的搜索方法是不可取的。为了解决这样的问题，我们需要用到Apriori算法来解决。

有关关联分析的一些应用

  1. 购物篮分析，这是关联分析最经典的一项应用。我们耳熟能详的尿布与啤酒就是来源于此（虽然这个故事的真实性有待考据，但这并不影响它成为一个营销界的小故事）。
  2. 公众热点发现
  3. 新闻及流行趋势挖掘
  4. 搜索引擎推荐
  5. 发现毒蘑菇的相似特征（该例子取自《机器学习实战》一书）

Apriori算法

优点：易编码实现
缺点：在大数据集上计算效果较慢

既然关联分析是一种在大规模数据集中寻找有趣的关系的任务。这些关系可以有两种形式：一种就是我们上面所说的频繁项集(frequent itemsets);另外一种则是关联规则(association rules)。关联规则，其暗示了两种物品之间可能存在很强的关系。

那么我们该如何定义有趣的关系呢？以及，频繁项集中的频繁有怎么划定呢？虽然，许多概念都可以说明这些问题，但是最重要及最通用的莫过于其支持度和可信度。

支持度(support)：一个项集的支持度被定义为数据集包含该项集的记录比例。

举个例子:
apriori.jpg
如上图所示，因为5项记录中有4条包含了{豆奶}，所以其支持度为4/5;依此类推，{豆奶，尿布}的支持读为3/5。

可信度或置信度(confidence)：这个概念是针对一条{尿布} -> {葡萄酒}这样的关联规则来定义的。

支持度和可信度是用来量化关联分析是否成功的方法。

Apriori原理

如果计算一个集合中的频繁项集的支持度，首先需要遍历全部可能的项集，比如针对一个包含了4个产品的集合，那么购买该集合产品的可能集合数目为2^4-1=15，而针对包含N项的集合，就需要遍历2^N-1。显然，这样的计算量很大。为了降低所需计算时间，就需要我们所谓的Apriori原理。

其基本思路：如果某个项集是频繁的，那么它的所有子集也是频繁的。该定理的逆反定理为：如果某一个项集是非频繁的，那么它的所有超集（包含该集合的集合）也是非频繁的。Apriori原理的出现，可以在得知某些项集是非频繁之后，不需要计算该集合的超集，有效地避免项集数目的指数增长，从而在合理时间内计算出频繁项集。

算法基本流程

当集合中项的个数大于0时：
创建一个长度为k的候选项集列表
检查数据以确认每个项集都是频繁的
保留频繁项集，并构建k+1项组成的候选集列表

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

def load_dataset():
    "Load the sample dataset."
    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
def createC1(dataset):
    "Create a list of candidate item sets of size one."
    c1 = []
    for transaction in dataset:
        for item in transaction:
            if not [item] in c1:
                c1.append([item])
    c1.sort()
    #frozenset because it will be a ket of a dictionary.
    return list(map(frozenset, c1))
def scanD(dataset, candidates, min_support):
    "Returns all candidates that meets a minimum support level"
    sscnt = {}
    for tid in dataset:
        #print(tid)
        for can in candidates:
            if can.issubset(tid):
                sscnt.setdefault(can, 0)
                sscnt[can] += 1

    num_items = float(len(dataset))
    retlist = []
    support_data = {}
    for key in sscnt:
        support = sscnt[key] / num_items
        if support >= min_support:
            retlist.insert(0, key)
        support_data[key] = support
    return retlist, support_data
def aprioriGen(freq_sets, k):
    "Generate the joint transactions from candidate sets"
    retList = []
    lenLk = len(freq_sets)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            L1 = list(freq_sets[i])[:k - 2]
            L2 = list(freq_sets[j])[:k - 2]
            L1.sort()
            L2.sort()
            if L1 == L2:
                retList.append(freq_sets[i] | freq_sets[j])
    return retList


def apriori(dataset, minsupport=0.5):
    "Generate a list of candidate item sets"
    C1 = createC1(dataset)
    D = list(map(set, dataset))
    L1, support_data = scanD(D, C1, minsupport)
    L = [L1]
    k = 2
    while (len(L[k - 2]) > 0):
        Ck = aprioriGen(L[k - 2], k)
        Lk, supK = scanD(D, Ck, minsupport)
        support_data.update(supK)
        L.append(Lk)
        k += 1
    return L, support_data

挖掘关联规则

上面，我们实现了用apriori算法找出了频繁项集。现在我们来尝试找出关联规则。那么什么是关联规则呢？我们可以举这样一个例子：假设我们有一个频繁项集是：{豆奶，莴苣}。那么则意味着一个人如果他已经购买了豆奶，那么他也有很大的几率会购买莴苣;但反过来却不一定成立：则如果一个人购买了莴苣，但还是不能说明他有很大几率会接着购买豆奶。

既然，在上面的例子中我们已经用支持度作为一种参考单位去量化一个集合的频繁关系，在这里我们同理也可以通过另一个概念来度量关联规则。没错，它就是我们已经在上面提过的可信度。根据可信度的计算法则和定义可知：

这也是我们上面已经提及过的问题。加上，在上面的例子之中我们已经得到了所有的频繁项集的支持度，那么为了求出各关联规则的可信度也就是剩下一个除法的问题而已。

如何从频繁项集中生成关联规则

一般对于一个频繁项集而言，如果我们直接生成关联规则的话，往往会有很多条。例如：我们对一个频繁项集{0，1，2，3}直接生成关联规则的话结果就如下图所示一样：
assrule.png
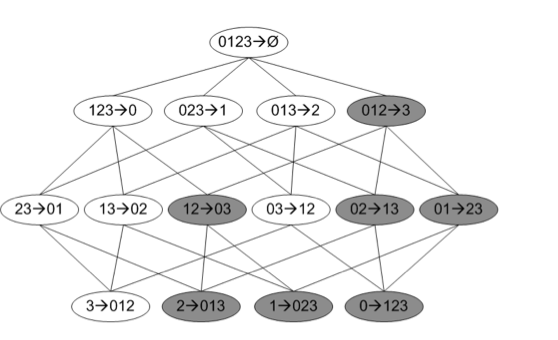
从上图我们就可以看出仅仅含4项的频繁项集就会生成出如此多的关联规则，那么如果频繁项集中含有10，20，甚至100个元素那么生成的候选关联规则的数据是相当庞大。

在此，我们可以参考apriori算法中挖掘频繁项集的思路。在发现频繁项集时我们通过最低支持度的方法来忽略掉一些项集支持度的计算;同理，在这里我们将这个思想应用在关联规则的生成之上，即：如果一条规则的不满足最低可信度的要求，那么其子集自然也不能满足最低可信度的要求。对于这部分规则的可信度计算我们可以直接忽略。如上图中的阴影部分。我们假设规则{0，1，2} -> 3不能满足最低可信度，那么，他的子集{1，2}->{0，3}，{0，2}->{1，3}等将不能满足最低可信度。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

def generateRules(L, support_data, min_confidence=0.7):
    """Create the association rules
    L: list of frequent item sets
    support_data: support data for those itemsets
    min_confidence: minimum confidence threshold
    """
    rules = []
    for i in range(1, len(L)):
        for freqSet in L[i]:
            H1 = [frozenset([item]) for item in freqSet]
            print("freqSet", freqSet, 'H1', H1)
            if (i > 1):
                rules_from_conseq(freqSet, H1, support_data, rules, min_confidence)
            else:
                calc_confidence(freqSet, H1, support_data, rules, min_confidence)
    return rules


def calc_confidence(freqSet, H, support_data, rules, min_confidence=0.7):
    "Evaluate the rule generated"
    pruned_H = []
    for conseq in H:
        conf = support_data[freqSet] / support_data[freqSet - conseq]
        if conf >= min_confidence:
            print(freqSet - conseq, '--->', conseq, 'conf:', conf)
            rules.append((freqSet - conseq, conseq, conf))
            pruned_H.append(conseq)
    return pruned_H


def rules_from_conseq(freqSet, H, support_data, rules, min_confidence=0.7):
    "Generate a set of candidate rules"
    m = len(H[0])
    if (len(freqSet) > (m + 1)):
        Hmp1 = aprioriGen(H, m + 1)
        Hmp1 = calc_confidence(freqSet, Hmp1,  support_data, rules, min_confidence)
        if len(Hmp1) > 1:
            rules_from_conseq(freqSet, Hmp1, support_data, rules, min_confidence)

运行测试

1
2
3

dataset = load_dataset()
L,support_data = apriori(dataset)
generateRules(L,support_data)

输出结果
freqSet frozenset({3, 5}) H1 [frozenset({3}), frozenset({5})]
freqSet frozenset({1, 3}) H1 [frozenset({1}), frozenset({3})]
frozenset({1}) —> frozenset({3}) conf: 1.0
freqSet frozenset({2, 5}) H1 [frozenset({2}), frozenset({5})]
frozenset({5}) —> frozenset({2}) conf: 1.0
frozenset({2}) —> frozenset({5}) conf: 1.0
freqSet frozenset({2, 3}) H1 [frozenset({2}), frozenset({3})]
freqSet frozenset({2, 3, 5}) H1 [frozenset({2}), frozenset({3}), frozenset({5})]
Out[6]:
[(frozenset({1}), frozenset({3}), 1.0),
(frozenset({5}), frozenset({2}), 1.0),
(frozenset({2}), frozenset({5}), 1.0)]

从输出结果可以看出，其中{1} —> {3}，{5} —> {2}，{2} —> {5}这三条关联规则的可信度居然达到了1.0，而且{2}，{5}还存在一个相互关联的关系。除此之外，我们还可以发现：虽然{1} —> {3}这条关联的可信度达到了1.0，但是{3} —> {1}却不足0.7（因为我们的最低可信度标准为0.7，没有输出显示的规则，则意味着它们的可信度低于0.7)。为了可以看见输出更多的规则，我们可以降低下最低可信度的标准，再来执行一遍代码。

1
2
3

dataset = load_dataset()
L,support_data = apriori(dataset)
generateRules(L,support_data,0.5)

输出结果
freqSet frozenset({3, 5}) H1 [frozenset({3}), frozenset({5})]
frozenset({5}) —> frozenset({3}) conf: 0.6666666666666666
frozenset({3}) —> frozenset({5}) conf: 0.6666666666666666
freqSet frozenset({1, 3}) H1 [frozenset({1}), frozenset({3})]
frozenset({3}) —> frozenset({1}) conf: 0.6666666666666666
frozenset({1}) —> frozenset({3}) conf: 1.0
freqSet frozenset({2, 5}) H1 [frozenset({2}), frozenset({5})]
frozenset({5}) —> frozenset({2}) conf: 1.0
frozenset({2}) —> frozenset({5}) conf: 1.0
freqSet frozenset({2, 3}) H1 [frozenset({2}), frozenset({3})]
frozenset({3}) —> frozenset({2}) conf: 0.6666666666666666
frozenset({2}) —> frozenset({3}) conf: 0.6666666666666666
freqSet frozenset({2, 3, 5}) H1 [frozenset({2}), frozenset({3}), frozenset({5})]
frozenset({5}) —> frozenset({2, 3}) conf: 0.6666666666666666
frozenset({3}) —> frozenset({2, 5}) conf: 0.6666666666666666
frozenset({2}) —> frozenset({3, 5}) conf: 0.6666666666666666
Out[7]:
[(frozenset({5}), frozenset({3}), 0.6666666666666666),
(frozenset({3}), frozenset({5}), 0.6666666666666666),
(frozenset({3}), frozenset({1}), 0.6666666666666666),
(frozenset({1}), frozenset({3}), 1.0),
(frozenset({5}), frozenset({2}), 1.0),
(frozenset({2}), frozenset({5}), 1.0),
(frozenset({3}), frozenset({2}), 0.6666666666666666),
(frozenset({2}), frozenset({3}), 0.6666666666666666),
(frozenset({5}), frozenset({2, 3}), 0.6666666666666666),
(frozenset({3}), frozenset({2, 5}), 0.6666666666666666),
(frozenset({2}), frozenset({3, 5}), 0.6666666666666666)]

这次我们就可以在输出中看见{3} —> {1}了，它的可信度为0.6666666666666666。

到此，有关关联分析的apriori算法就告一段落了。后续还会有有关关联分析FP-growth算法的文章讲解。