SVM(Support Vector Machines)-支持向量机

曾经很多人都认为SVM是现在的最好的分类器，即：在不加以修改的前提之下，就能够在数据上进行训练并能够对训练集之外的数据点做出很好的分类决策。

基于最大间隔分割数据

支持向量机：
优点：泛化错误率低，计算开销不大，结果容易解释
缺点：对参数调节和核函数的选择策略敏感，原始分类器不加修改仅适用于处理二类问题。

在上图中，我们可以看出：我们可以很容易在图中画出一条直线将两组数据点分开。在这种情况下，这组数据被称为线性可分(linearly separable)数据，而将数据集分割开来的直线我们称为分隔超平面(separating hyperplane)。在上图例子中，由于数据点都在二维平面上，所有此时分隔超平面就只是一条直线而已。但是，如果所给的数据为三维的，那么此时用来分隔数据的就是一个平面。依此类推，如果给出一个N（N>3）维数据集，那么则要用一个N-1维的对象来对数据进行分隔，该对象亦被称为超平面(hyperplane)。

我们希望通过这样的方式来构建分类器。即如果数据点离决策边界越远，那么其最后的预测效果就越可信。那么我们继续看回上面的图片，我们可以看到有三条直线（一条实线，两条虚线）它们分别都能将数据分隔开，但是其中哪一条才是最理想的呢？通常，我们可以做过这样的方法来确定一个最佳分隔平面，即：我们先找到离分隔平面最近的点，确保它们离分隔平面的距离尽可能远。

这里我们又要先引入一些新的概念：
首先是，点到分隔面的距离被称为间隔(margin)
支持向量(support vector)：就是离分割平面最近的那些点。

接下来，就是最大化支持向量都分隔面的距离，并需要找到此问题的优化求解方法。

寻找最大间隔

Maximum Marginal（最大间隔）是SVM的一个理论基础之一。选择使得间隔最大的函数作为分隔平面是十分容易解释的。从概率的角度上而言，就是使得置信度最小的点置信度最大;从现实意义上而言，两个个体的类别差异越大，我们自然也能够更为准确地分类。

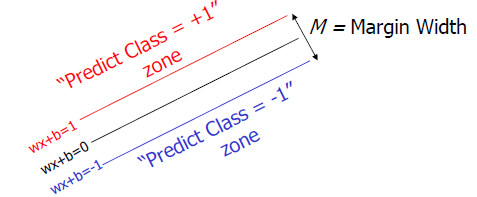
上图就是一个对之前所提及的类别间隙的一个描述。其中中间的黑色实线为分隔边界（Classifier Boundary）是我们算法中要求解的f(x)，红色和蓝色的线(plus plane 与 minus plane)就是支持变量所在的平面，而红色，蓝色之间的间隙就是我们要最大化的分类间的间隙。

首先，我们可以知道其两个支持向量的所在平面可以表达成如下形式：

和

然后，这两个超平面的距离可以表达成：

因此，为了最大化两个平面的距离，我们只要最小化即可。

综上所述，我们可以将整个原理表示为：

Minimize
subject to
for

当支持变量确定的时候，整个分割函数也就确定了下来。除此之外，支持向量的出现还可以让向量后方的样本点不用再参与计算，大大降低了算法的计算复杂度。

再者，有关距离计算的优化。$||\vec w||$的意思是$\vec w$的二范数，由之前我们得到的最大间隔$M=2/||\vec w||$，最大化这个式子等价于最小化$|||\vec w||$，另外由于$||\vec w||$是一个单调函数，我们可以对其进行平方，和加上系数。数学经验丰富的朋友可能一眼就看出来，这样做是为了方便求导。

最后我们的式子可以写成：

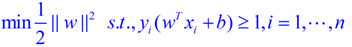
s.t的意思是subject to，也就是在后面这个限制条件下的意思，这个词在svm的论文里面非常容易见到。这其实是一个带约束的二次规划(quadratic programming, QP)问题，是一个凸问题，凸问题就是指的不会有局部最优解，可以想象一个漏斗，不管我们开始的时候将一个小球放在漏斗的什么位置，这个小球最终一定可以掉出漏斗，也就是得到全局最优解。s.t.后面的限制条件可以看做是一个凸多面体，我们要做的就是在这个凸多面体中找到最优解。

优化求解

这个优化问题可以用拉格朗日乘子法去解，使用了KKT条件的理论，这里直接作出这个式子的拉格朗日目标函数：

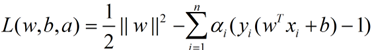
由于求解这个式子的过程需要拉格朗日对偶性的相关知识，以及较深入的数学背景知识，在这篇文章中暂且不谈，以后博客再另外写一篇有关具体推导的文章。

在此，我先贴出在该问题在论文中的关键推导步骤：

上图就是我们需要最终优化的式子了。整篇文章到这里，我们终于得到了SVM线性可分问题的优化式子。

SVM的使用

由于支持向量机算法的实现涉及过多的数学背景，在本中暂不使用原生程序代码实现，而是选择调用Python sklearn 库现有的SVM算法进行使用的举例。

1
2
3
4
5
6
7
8
9
10

from sklearn import svm
from sklearn import datasets
from sklearn import metrics
clf = svm.SVC()
print(clf)
iris = datasets.load_iris()
X, y = iris.data, iris.target
clf.fit(X, y)
pred = clf.predict(X)
print(metrics.accuracy_score(y,pred))

输出结果
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma=’auto’, kernel=’rbf’,
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
0.986666666667

本例使用的是sklearn库自带的iris数据集使用SVM算法进行训练，然后再进行回测。首先，我们可以看到在不做任意处理的前提下，SVM模型的预估效果也是相当不错的，其准确率高达98%（其结果主要因为使用的数据集优秀导致的，直接运用于工程上时不会有这么高的准确率）。

当然，上面例子中的算法模型的实现方式是十分简陋的。如果真正要使用SVM进行严格地建模，测试集与训练集的划分问题，数据的归一化处理问题等。都是我们需要考虑的元素。但由于本文主要为了介绍与探讨SVM算法，其他细节问题就不一一处理，详细方法可以参考我写的其他文章。

SVM的其他实现

除了Python的sklearn库外，SVM在其它语言及平台也有实现。其中：
最流行的有

LIBSVM：https://www.csie.ntu.edu.tw/~cjlin/libsvm/
这是经典的svm库支持多种语言调用

再者，在R语言中也有SVM算法的实现：

e1071：
https://cran.r-project.org/web/packages/e1071/index.html