隐马尔可夫模型(HMM)的原理
简介
隐马尔可夫模型是一个基于马尔可夫链的统计模型。
马尔可夫链因安德烈·马尔可夫(Andrey Markov,1856-1922)得名,是数学中具有马尔可夫性质的离散时间随机过程。该过程中,在给定当前知识或信息的情况下,过去(即当期以前的历史状态)对于预测将来(即当期以后的未来状态)是无关的。
虽然从维基百科上摘取下来的概念和定义看着十分的晦涩难懂,但是模型背后的思想是非常简单的,即:首先假设你的系统可以建模为马尔可夫链,然后,系统所发出的信号(输出的可见结果)仅取决于系统当前的状态。那么,隐马尔可夫模型代表的一种情景就是:系统的状态对你而言是不可见的,你仅仅只能观测到系统所发出的信号或者说是系统所输出的结果。
举个通俗易懂的栗子。
假设你有一个住在国外的朋友,他通常会根据天气来安排他的日常活动。你不知道他的国家那边的天气如何(系统的状态),但你确可以在跟他的聊天中知道他今天进行了什么活动(系统的输出),然后这就是一个简单的隐马尔可夫模型。
我们将整个模型
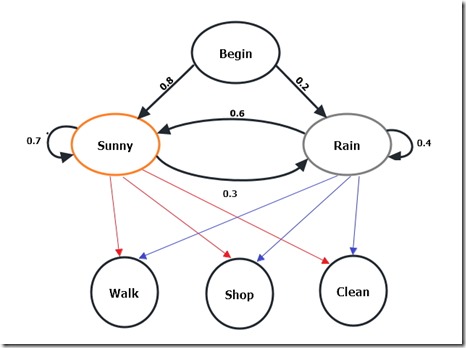
现在有三个比较关键的问题有待我们解决:
1. 知道整个模型后,你朋友告诉你他这三天的活动是:散步(Walk),购物(Shop),清洁屋子(Clean),那么根据模型,计算产生这些行为序列的概率是多少?
2. 知道整个模型后,朋友让你根据他的活动猜一猜他那边这三天天气怎么样
3. 朋友告诉你三天里他做了些什么,然后让你找出他活动规律的模型。
为了解决以上的问题我们首先要了解一些有关HMM的基本元素先:
初始概率分布:初始概率分布即事件初始时发生的概率,我们这里隐藏的状态是天气,然后我们在图中可以看出的初始概率有:天气为晴天的概率为0.8 ; 天气为雨天的概率为0.2
转移概率矩阵P:转移功率矩阵就可以通过一副图来描述了。
| 晴天 | 雨天 |
|---|---|
| 晴天 | 0.7 |
| 雨天 | 0.6 |
其中,列参数表示第一天的状态,行参数表示第二天状态。表格中的第一行的含义就是已知第一天为晴天,那么第二天为晴天的概率是0.7,而为雨天的概率只是0.3。
观测量的概率分布B:在这个问题中观测量就是朋友的活动,其概率分布就分别表示为朋友在晴天和雨天的情况下进行散步,购物,打扫屋子各项活动的可能性(概率)。
现在,我们再次回到上面提到的三个问题。其实,每个问题的解决解决在历史上早有前人给出了算法。
问题1 -> Forward Algorithm,向前算法 或 Backward Algorithm,向后算法。
问题2 -> Viterbi Algorithm,维特比算法。
问题3 -> Baum-Welch Algorithm,鲍姆-维尔奇算法。
算法思路
假设前提:
已知,雨天,朋友选择去散步,购物,收拾的概率分别是0.1,0.4,0.5, 而如果是晴天,选择去散步,购物,收拾的概率分别是0.6,0.3,0.1。
三天活动序列:散步(Walk),购物(Shop),清洁屋子(Clean)
Forward Algorithm
然后我们先计算 t = 1 时,发生 “散步” 行为的概率,如果下雨,则;如果为晴天,则
t = 2 时,发生 “购物” 的概率,如果 t = 2 下雨,则
如果为晴天,则
t = 3 时的算法也可以依此类推,
;
所以,最终:
从上面的例子可以看出,向前算法计算了每个时间点时,每个状态的发生观测序列的概率,看似复杂,但在T变大时,复杂度也会随之降低。
Backward Algorihm
既然,向前算法是在时间 t = 1 的时候,一步一步向前计算。那么反过来,向后算法就是从最后一个状态往前推。
假设最初时
那么:
其中第一项则是转移概率,第二天下雨转到第三天下雨的概率为0.4;第二项则是观测概率,第三天下雨的状况下,在家收拾的概率为0.5;第三项就是我们定义的向后变量(backward variable)。
同理也可推得其他数据,并且最终答案与向前算法的求解相同。
Viterbi Algorithm(维比特算法)
利用动态规划求解概率最大的路径(最优路径)。利用动态规划,可以解决任何一个图中的最短路径问题。而维特比算法是针对一个特殊的图——篱笆网络的有向图(Lattice)的最短路径提出的。
我们假设用符号来表示系统的第 i 种状态的第j个可能的值。如果把每个状态按照不同的值展开,就可以得到以下的篱笆网络(Lattice):
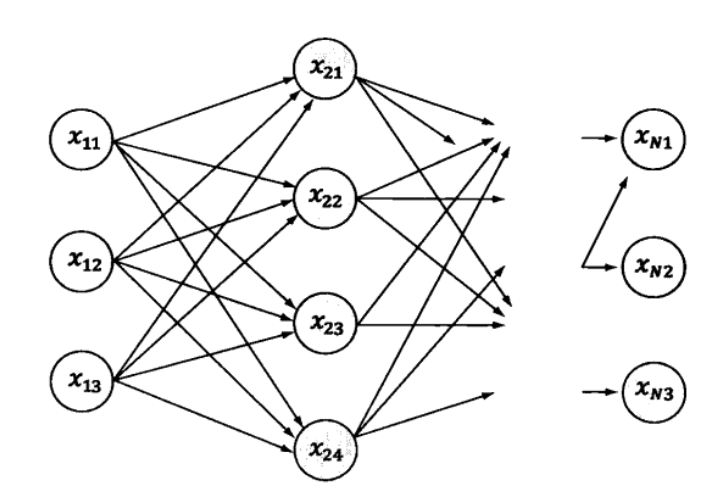
那么从第一个状态到最后一个状态的任何一条路径(path)都可能产生我们观察到的输出序列Y。当然,这些路径的可能性不一样,而我们要做的就是找到最可能的这条路径。对于每一条给定的路径我们都可以用公式:
计算出它的可能性,但是随着组合增多,它使得序列状态数的增长呈指数爆炸式。
为了解决这个问题,需要一个最好能和状态数成正比的算法。也就是我们要讲的维特比算法。
维特比算法的基础可以概括成三点:
如果概率最大的路径P(或者说最优路径)经过某个点,如果上图中的,那么这条路径上从起始点S 到 的这一段子路径Q,一定是S到的最短路径。否则用S到的最短路径R来代替Q,便构成了一条比P更短的路径。
从S到E的路径必定经过第i个时刻的某个状态,假定第i个时刻有k个状态,那么如果记录了从S到第i个状态的所以k个节点的最短路径,最终最短路径必经过其中的一条。这样,在任何时刻,只要考虑非常有限条最短路径即可。
结合上述两点,假定当我们从状态 i 进入状态 i + 1 时,从 S 到状态 i 上各个节点的最短路径已经找到,并且记录在这些节点上,那么在计算从起点 S 到第 i + 1 状态的某个节点的最短路径时,只要考虑从S到前一个状态 i 所有的 k 个节点的最短路径,以及从这 k 个节点到,j 的距离即可。
实现过程
- 从点S出发,对于第一个状态的各个节点,不妨假定有个。计算出 S 到它们的距离,其中代表任意状态 1 的节点。因为只有一步,所以这些距离都是S到它们各自的最短距离。
- 对于第二个状态的所有节点,要计算出从S到它们的最短距离。我们知道,对于特定的节点,从S到它的路径可以经过状态1的中任何一个节点,当然,对应的路径长度就是。由于 j 有种可能性,我们要一一计算,然后找到最小值。即:
- 这样对于第二状态的每个节点,需要次乘法计算。假定这个状态有个节点,把S这些节点的距离都算一遍,就有次计算。
接下来,类似地按照上述方法从第二个状态走到第三个状态,一直走到最后一个状态,就得到了整个网格从头到尾的最短路径。每一步计算的复杂度都和相邻两个状态各自的节点数目的乘积成正比,即。如果假定在这个隐含马尔可夫链中的节点最多的状态有D个节点,也就是说整个网络的宽度为D,那么任何一布的复杂度不超过,由于网络长度是N,所以整个维特比算法的复杂度是 ——本段推理节选自<<数学之美>>第二版