K-means聚类简介

前面介绍了不少监督学习的各类算法，那么这次我们就来认识和了解一下无监督学习。首先，K-means聚类算法就是一种无监督学习的算法。这就意味着他可以通过没有分类标记的数据学习出训练数据本身的分组信息。（其实他的本质就是自动的将属性/特征类似的数据归到统一类别）而其最后分成的组数则由参数K来决定。

算法基本步骤

1. 随机初始化K个簇心。用作标识各组数据。
2. 根据各个数据的特征/属性，将他们聚类到距离最接近的一个簇，并打上分类标识。
3. 根据加入的数据重新计算每个簇的质心（均值，Means）
4. 重复2，3步，直至最后所有数据被划分成k个簇。

从以后的步骤我们也可以充分地看出，再聚类完毕之前数据是没有分组和标识的，而是通过聚类来查找和分析被划分在一起的数据。

同时，每个簇的质心是定义组的特征的代表，我们往往可以通过一个簇的质心看出该分组的特征以及属性。从而判断出这个簇代表了一个怎么样的组。

应用领域

• 网站，App的用户群体聚类
• 信用卡诈骗监测（这个是利用了聚类算法的反原理，寻找离群值）
• 文章自动归类
• 图像归类
• 人群健康状态监测（同信用卡诈骗检测同原理）

此外，我们还可以通过监控数据点根据时间的变化而造成的组间切换现象找到状态变化的方法。

算法主要原理

（1）在数据划分方面，我们主要依赖的思路是：欧氏距离。即，每个簇的质心定义了一种聚类，然后每个点根据其到每个簇的质心的欧几里德距离的平方的大小，将其分配到最近的簇中。我们假设$c_i$是簇集合C中质心i，那么我们可以将其聚类的过程表达成下列形式：

$argmin_{c_i \in C} dist(c_i,x)^2$

（2）质心的更新，在这一步骤中，各个簇的质心将要被重新计算，通过加入新的数据再重新计算包括i新数据在内的的整个簇的均值以此作为新的质心。该过程可以表达为一下形式：

$c_i=\frac{1}{|S_i|}\sum_{x_i \in S_i }x_i$

在多次迭代之后，该算法可以保证收敛于一个结果，虽然有可能只是一个局部的最优解而已。为了使得最后结果更加稳定和可靠，我们也可以通过多次运行算法然后再在多个结果中取得一个均衡（为什么说多次计算可以得到更好的结果呢？ 因为每次随机初始化的质心都是不同的，这样使得每次的运行结果都不尽相同，为了得到一个更加稳定的结果和更好的鲁棒性，多次运行往往是一个简单但却有效的方法。）

有关K值的选择

在K-means聚类算法中，K值的选择往往是一个较为难以抉择的问题。最后的情况是，在你应用这个算法之前，已经知道数据应该分为多少个类别合适，或者将这种方法应用在一个半监督学习的场合，使得最后的分类结果有据可依。

那么，在一般我们不太清楚分类的情况之下，我们能做的就是通过为K值制定一个范围，然后在这个范围之上，我们尝试运行我们的分类器，然后根据分类效果来评判我们的k的取值。

另外一方面，聚类算法通常会不断降低各个样本点到质心之间的距离，随着k值的增加，“距离”更是一直下降。但是，当k值增大到一定程度时，虽然“距离”仍在下降，但下降的速率已经变得十分缓慢了。我们常常称这个点的k值为肘点。往往到达肘点的k值已经能够很好地将各个类别之间的差异信息给描述出来，所以我们可以在不清楚数据具体分类信息的情况下，选择肘点值来作为我们的k值。

Example

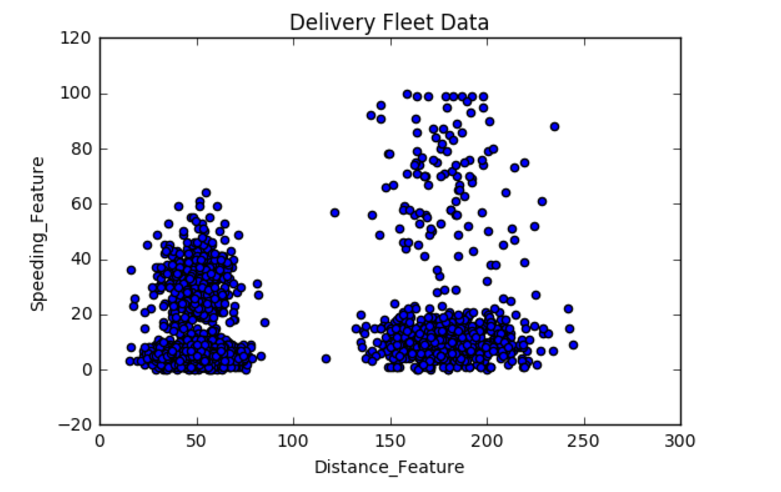
在这里我们通过Python的Sklearn库来看一下K-means的应用实例

Delivery Fleet Data 数据下载

数据读取

1
2
3
4
5
6
7
8
9

import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("data_1024.csv",sep='\t')
plt.scatter(df['Distance_Feature'],df['Speeding_Feature'])
plt.xlabel("Distance_Feature")
plt.ylabel("Speeding_Feature")
plt.title("Delivery Fleet Data")
plt.show()
df.head()

输出结果
Driver_ID Distance_Feature Speeding_Feature
0 3423311935 71.24 28.0
1 3423313212 52.53 25.0
2 3423313724 64.54 27.0
3 3423311373 55.69 22.0
4 3423310999 54.58 25.0

算法使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import numpy as np
from sklearn.cluster import KMeans
X_train = df[['Distance_Feature','Speeding_Feature']]
kmeas = KMeans(n_clusters=2).fit(X_train)

color = [str(item/255.) for item in kmeas.labels_]
plt.scatter(df['Distance_Feature'],df['Speeding_Feature'],c=color)
plt.xlabel("Distance_Feature")
plt.ylabel("Speeding_Feature")
plt.title("Delivery Fleet Data")
plt.show()
kmeas = KMeans(n_clusters=4).fit(X_train)

color = [str(item/255.) for item in kmeas.labels_]
plt.scatter(df['Distance_Feature'],df['Speeding_Feature'],c=color)
plt.xlabel("Distance_Feature")
plt.ylabel("Speeding_Feature")
plt.title("Delivery Fleet Data")
plt.show()

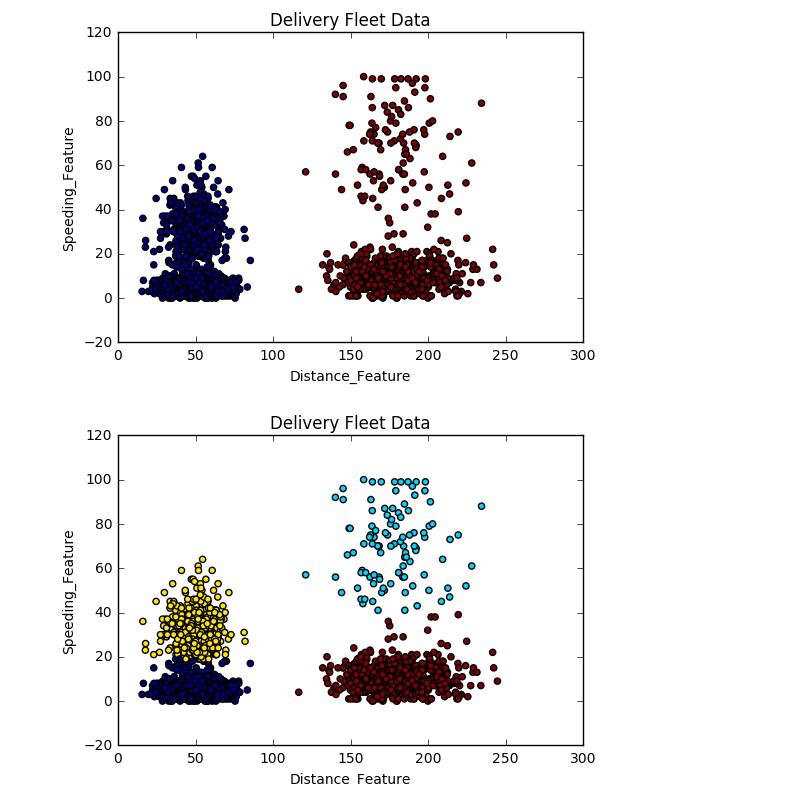
输出结果

上面的结果展示了，K分别等于2和4时对数据的聚类的结果，由于这个算法使用还算简单，在这里我也不做赘述了。那么有关K-means的简介到这里也就结束了，谢谢大家的阅读。