Python实现Fisher 判别分析

Fisher原理

费歇（Fisher）判别思想是投影，使多维问题化为一维问题来处理。选择一个适当的投影轴，使所有的样本点都投影在这个轴上得到一个投影值。对这个投影轴的方向的要求是：使每一类内的投影值所形成的类内距离差尽可能小，而不同类间的投影值所形成的类间距离差尽可能大。

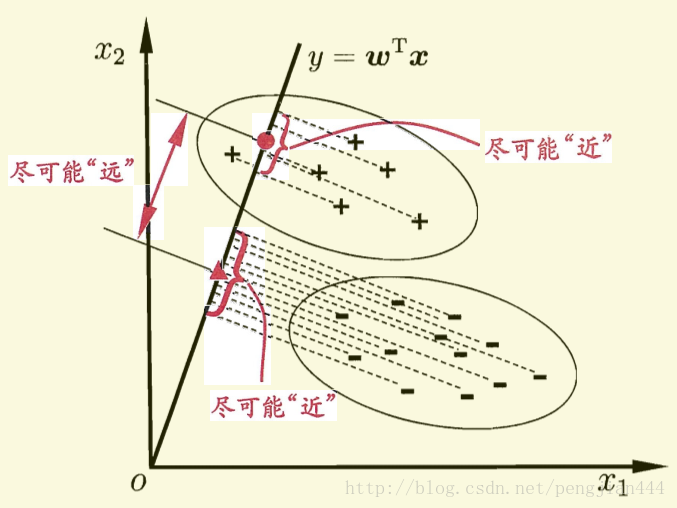
这样如果我们想要同类样列的投影点尽可能接近，可以让同类样列投影点的协方差尽可能小，即$w^T \left(\sum _0 w\right)+w^T \left(\sum _1 w\right)$尽可能小;而欲使异类样列的投影点尽可能远离，可以让类中心之间的距离尽可能大，即$\left[\left[u_0 w^T-u_1 w^T\right]\right]$尽可能大。同时结合两者我们可以得到欲最大化的目标：

(本文图片截取自《机器学习》周志华)

有了上面的推理之后我们接下来就以DNA分类为例来实现一下Fisher线性判别。

数据准备

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

from sklearn.cross_validation import train_test_split
dna_list = []
with open('dna2','r') as f:
    dna_list = list(map(str.strip,f.readlines()))
    f.close()
print(len(dna_list))
def generate_feature(seq):
    for i in seq:
        size = len(i)
        yield [
        chary.count(i,'a')/size,
        chary.count(i,'t')/size,
        chary.count(i,'c')/size,
        chary.count(i,'g')/size]

X = np.array(list(generate_feature(dna_list)),dtype=float)
y = np.ones(20)
y[10:]=2
X_train, X_test, y_train, y_test = train_test_split(X[:20], y, test_size=0.1)
print(X_train,'\n',y_train)

输出结果：
40
[[ 0.2972973 0.13513514 0.17117117 0.3963964 ]
[ 0.35454545 0.5 0.04545455 0.1 ]
[ 0.42342342 0.28828829 0.10810811 0.18018018]
[ 0.35135135 0.12612613 0.12612613 0.3963964 ]
[ 0.27927928 0.18918919 0.16216216 0.36936937]
[ 0.21818182 0.56363636 0.14545455 0.07272727]
[ 0.20720721 0.15315315 0.20720721 0.43243243]
[ 0.3 0.5 0.08181818 0.11818182]
[ 0.2 0.56363636 0.17272727 0.06363636]
[ 0.27027027 0.06306306 0.21621622 0.45045045]
[ 0.32727273 0.5 0.02727273 0.14545455]
[ 0.23423423 0.10810811 0.23423423 0.42342342]
[ 0.29090909 0.64545455 0. 0.06363636]
[ 0.18181818 0.13636364 0.27272727 0.40909091]
[ 0.29090909 0.5 0.11818182 0.09090909]
[ 0.25454545 0.51818182 0.1 0.12727273]
[ 0.27433628 0.36283186 0.19469027 0.16814159]
[ 0.27027027 0.15315315 0.16216216 0.41441441]]
[ 1. 2. 1. 1. 1. 2. 1. 2. 2. 1. 2. 1. 2. 1. 2. 2. 2. 1.]

Fisher算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

def cal_cov_and_avg(samples):
    """
    给定一个类别的数据，计算协方差矩阵和平均向量
    :param samples: 
    :return: 
    """
    u1 = np.mean(samples, axis=0)
    cov_m = np.zeros((samples.shape[1], samples.shape[1]))
    for s in samples:
        t = s - u1
        cov_m += t * t.reshape(4, 1)
    return cov_m, u1


def fisher(c_1, c_2):
    """
    fisher算法实现(请参考上面推导出来的公式，那个才是精华部分)
    :param c_1: 
    :param c_2: 
    :return: 
    """
    cov_1, u1 = cal_cov_and_avg(c_1)
    cov_2, u2 = cal_cov_and_avg(c_2)
    s_w = cov_1 + cov_2
    u, s, v = np.linalg.svd(s_w)  # 奇异值分解
    s_w_inv = np.dot(np.dot(v.T, np.linalg.inv(np.diag(s))), u.T)
    return np.dot(s_w_inv, u1 - u2)

判别类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

def judge(sample, w, c_1, c_2):
    """
    true 属于1
    false 属于2
    :param sample:
    :param w:
    :param center_1:
    :param center_2:
    :return:
    """
    u1 = np.mean(c_1, axis=0)
    u2 = np.mean(c_2, axis=0)
    center_1 = np.dot(w.T, u1)
    center_2 = np.dot(w.T, u2)
    pos = np.dot(w.T, sample)
    return abs(pos - center_1) < abs(pos - center_2)


w = fisher(X_train[:10], X_train[10:20])  # 调用函数，得到参数w
pred = []
for i in range(20):
    pred.append( 1 if judge(X[i], w, X_train[:10], X_train[10:20]) else 2)   # 判断所属的类别
# evaluate accuracy
pred = np.array(pred)
print(y,pred)
print(metrics.accuracy_score(y, pred))
out = []
for i in range(20,40):
    out.append( 1 if judge(X[i], w, X_train[:10], X_train[10:20]) else 2)   # 判断所属的类别
print(out)

输出结果：
[ 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 2. 2. 2. 2. 2. 2. 2. 2.
2. 2.] [1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 1]
0.95
[1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1]

在这我们可以看出我们的Fisher算法在测试集中的误差率还算理想，误判率仅有5%。但是，我们可以看出其预测分类并不如其他KNN，SVM，等算法的预测效果。

最后，有关Fisher算法的介绍也就到此结束了！

K-近邻算法-Part2

使用交叉验证来调整k值

通常来说,一个最优的KNN模型其k参数所对应的预估错误率应该是最低的。因此，在选定模型k值的时候应该反复尝试不同的k值在预估上的效果，对比其错误率。初学者在这里为了降低模型的误差通常会将全部样本数据也作为训练集一起代入模型进行训练。虽然这种做法在训练时确实能够有效降低误差，对现有数据进行更好的拟合。但是，同时带来的后果是：我们会将数据的各种无法避免的真实误差，如测量误差，抽样误差等也训练进了我们的模型之中，使得训练出来的模型在新数据或未知数据上的预估效果特别差，这种现象也被称为过拟合（overfitting）。

为了降低预估的错误率以及避免过拟合现象的发生，我们可以在某种意义下将原始数据(dataset)进行分组,一部分做为训练集(train set),另一部分做为验证集(validation set or test set)，首先用训练集对分类器进行训练,再利用验证集来测试训练得到的模型(model),以此来做为评价分类器的性能指标。这种方法也就是所谓的交叉验证（Cross Validation）。

而在交叉验证中，K折交叉验证（k-fold cross validation）是比较常用的。其主要思想是：初始采样分割成K个子样本，一个单独的子样本被保留作为验证模型的数据，其他K-1个样本用来训练。交叉验证重复K次，每个子样本验证一次，平均K次的结果或者使用其它结合方式，最终得到一个单一估测。这个方法的优势在于，同时重复运用随机产生的子样本进行训练和验证，每次的结果验证一次，10折交叉验证是最常用的。

为了更好的理解k折交叉验证，我们继续沿用part1部分的训练数据，使用10折交叉验证的方法来调整我们的k值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

import matplotlib.pyplot as plt
from sklearn.cross_validation import cross_val_score
# creating odd list of K for KNN
myList = list(range(1,50))

# subsetting just the odd ones
neighbors = list(filter(lambda x: x % 2 != 0, myList))

# empty list that will hold cv scores
cv_scores = []

# perform 10-fold cross validation
for k in neighbors:
    knn = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn, X_train, y_train, cv=10, scoring='accuracy')
    cv_scores.append(scores.mean())

# changing to misclassification error
MSE = [1 - x for x in cv_scores]

# determining best k
optimal_k = neighbors[MSE.index(min(MSE))]
print ("The optimal number of neighbors is %d" % optimal_k)

# plot misclassification error vs k
plt.plot(neighbors, MSE)
plt.xlabel('Number of Neighbors K')
plt.ylabel('Misclassification Error')
plt.show()

在上面的程序中，我们在1-50的奇数中选取k值，并根据k值训练模型进行预估验证。最后根据不同k值训练出去的模型的均方误差（Mean Squared Error, MSE）作出折线图，并求出使得MSE最小的最优k值。

输出结果:

The optimal number of neighbors is 7

由此我们可以得出：在这个模型中，10折交叉验证告诉我们最优的k值是7。

尝试自己实现KNN算法

到目前为止，我们都是调用sklearn库中的KNN来完成分类任务。那么，下面我们来尝试自己实现一个简单的KNN算法并用它来分类我们之前的数据。

经过上一篇文章的介绍，我们可以知道KNN算法的关键是计算出新的待分类数据与现有的样本数据的“距离”，而其中较为常用的还是欧式距离（euclidean distance ）。然后提取出k个最相邻的点，并根据他们大多数点的分类属性来给待分类点进行归类。

因此核心计算代码我们可以这样写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

def predict(X_train, y_train, x_test, k):
  # create list for distances and targets
  distances = []
  targets = []

  for i in range(len(X_train)):
      # first we compute the euclidean distance
      distance = np.sqrt(np.sum(np.square(x_test - X_train[i, :])))
      # add it to list of distances
      distances.append([distance, i])

  # sort the list
  distances = sorted(distances)

  # make a list of the k neighbors' targets
  for i in range(k):
      index = distances[i][1]
      targets.append(y_train[index])

  # return most common target
  return Counter(targets).most_common(1)[0][0]

在上面的代码中，我们首先创建一个保存距离的数组，并在存储完计算出的待测点与各样本点的距离后对数组进行升序排列，然后取出前k个最接近待测点的样本点，返回其出现最多的分类标签。

然后接下来让我继续完成整个KNN算法。

1
2
3
4
5

def kNearestNeighbor(X_train, y_train, X_test, predictions, k):

  # loop over all observations
  for i in range(len(X_test)):
      predictions.append(predict(X_train, y_train, X_test[i, :], k))

使用我们上面得出最优的 k = 7作为参数生成模型并进行预估。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# making our predictions 
from sklearn.metrics import accuracy_score
predictions = []

kNearestNeighbor(X_train, y_train, X_test, predictions, 7)

# transform the list into an array
predictions = np.asarray(predictions)
#print(y_test,predictions)
# evaluating accuracy
#for i in range(predictions.size):
#    print(predictions.tolist()[i],list(y_test)[i])
accuracy = accuracy_score(y_test, predictions)
print('\nThe accuracy of our classifier is %d%%' % int(accuracy*100))

输出结果： The accuracy of our classifier is 98%

到此，我们基本已经完成了一个类似于sklearn库中的KNN算法了，并且还有不错的准确率。

小结

最后，KNN算法介绍性文章到这就结束了。我们来总结一下KNN算法的优点与不足。

优点

• 易于理解
• 无需训练
• 容易迁移至多分类情况

不足

• 计算量大，时间复杂度随数据规模增大而增大
• 分类情况容易受高频分类影响

K-近邻算法-Part1

概述

K-近邻算法，即K-近邻分类算法，简称KNN其通过采用测量不同的特征值之间的距离方法进行分类。

有关K-近邻算法的问题

优点：精度高，对异常值不敏感，无数据输入假定

缺点：计算复杂度较高，空间复杂度较高

适用数据范围：数值型和标称型

工作原理

存在一个样本数据集合，即训练样本集，并且训练样本中的每一个数据都存在标签，我们可以清楚地知道每一个数据条目其与对应分类的所属关系。

然后在接受没有标记的新数据输入时，将新数据的特征提取出来将其一一与训练样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似的（即所谓的最近邻）的分类标签来作为新数据的标签。

其中为了避免偶尔性和离群值造成的误差因此有了以样本数据集中前k个最相似的数据作为判别的参考的标准这种做法。通常k是不大于20的整数而且一般选取奇数作为k值（奇数可以在投票分类时避免出现等票的情况），最终的分类结果由k个样本的分类标签投票形成，出现最多的分类标签作为新数据的分类。

一般算法流程

1. 收集数据
2. 准备数据：对数据进行清洗和结构化处理，使得数据可以进行距离计算
3. 分析数据：提取相关特征
4. 训练分类：knn算法并不需要训练
5. 测试算法：计算错误率
6. 使用算法：将新数据输入进行对应结构化之后，运行算法进行判定分类情况，并对后续的分类结果进行进一步处理应用

用KNN 制作简单的分类器

使用数据：UCI的鸢尾花数据集
点击进入目标链接后:

按照 Download Data Folder > iris.data 路径来下载指定数据集

准备数据

在这里我们使用Python 的 Pandas 包以没有标题栏的csv文件的形式读入数据

关键函数：read_csv

1
2
3
4
5
6
7
8
9

# loading libraries
import pandas as pd

# define column names
names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'class']

# loading training data
df = pd.read_csv('iris.data.txt', header=None, names=names)
df.head()

输出：

构建算法

距离函数

我a们在上面的例子中把一个很重要的概念隐藏了起来，在选择一个数量k还只是小问题，更重要的是距离的计算方法。毕竟，当我们说“最近的k个点”时，这个“近”是怎么衡量的？

在数学中，一个空间上距离的严格定义如下：
设 M 为一个空间，M上的一个距离函数是一个函数$d:M\times M \rightarrow R$，满足：

• $d(x,y)≥0 ∀x,y∈M$
• $d(x,y)=0⟺x=y$
• $d(x,y)=d(y,x) ∀x,y∈M$
• $d(x,z)≤d(x,y)+d(y,z) ∀x,y,z∈M$

两个点 x,y 之间的距离就是$d(x,y)$。

我们一般最常用的距离函数是欧氏距离，也称作$L_2$距离。

如果
$x=(x1,x2,…,xn)$ 和 $y=(y1,y2,…,yn)$是 n 维欧式空间 Rn 上的两个点，那它们之间的$L_2$距离是

$d_2(X,Y)=\sqrt{\sum _{i=1}^n \left(X_i-Y_i\right){}^2}$

由于Python 的scikit-learn包已经实现了KNN算法，因此我们在这里可以直接调用。

在scikit-learn中，需要以matrix的形式和目标向量的形式来导入和训练数据。

因此在使用scikit-learn之前需要做额外的数据结构处理，同时还应该把原数据划分成训练数据和测试数据这样更加有利于我们下面的算法正确率评估。

1
2
3
4
5
6
7
8
9
10

# loading libraries
import numpy as np
from sklearn.cross_validation import train_test_split

# create design matrix X and target vector y
X = np.array(df.ix[:, 0:4])   # end index is exclusive
y = np.array(df['class'])   # another way of indexing a pandas df

# split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

最后，我们根据划分好的数据集来构建真正的分类器，并用构建出来的分类器来进行数据拟合以及评估他的正确率。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# loading library
from sklearn.neighbors import KNeighborsClassifier
from sklearn import metrics
# instantiate learning model (k = 3)
knn = KNeighborsClassifier(n_neighbors=3)

# fitting the model
knn.fit(X_train, y_train)

# predict the response
pred = knn.predict(X_test)

# evaluate accuracy
# print(y_test,pred)
print(metrics.accuracy_score(y_test, pred))

输出

0.98

由此可见，在适用的场合之下，KNN分类器的准确率也是可以达到一个较为理想的水平的。

机器学习概论-科普篇

什么是机器学习？

机器学习是一门多领域交叉学科。专门研究计算机或其他软硬件设备怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有知识结构使不断改善自身的性能。

机器学习的应用领域

机器学习是人工智能研究的核心内容。它的应用已遍及人工智能的各个分支。如：专家系统，自动推理，自然语言处理，模式识别，计算机视觉，智能机器人等领域。

机器学习与数据挖掘的区别

机器学习在数据挖掘中被大量使用，其技术内涵几乎通用，可以看作同一座山峰在不同角度下的侧影。

机器学习与统计学的关系

机器学习和统计学是非常接近的两个领域。根据 Michael I. Jordan在机器学习领域的理念，从方法论原则到理论工具，在统计学领域是有一段很长的史前史。他也建议数据科学这一术语作为全部领域的前置。 Leo Breiman区别两个统计学的模型：数据模型和算法模型，在算法模型中意味着或多或少包含着机器学习的算法，比如随机森林（Random forest）。 一些统计学家已经采纳了机器学习中的一些做法，引申出了一个联结领域—–统计学习。

机器学习方法

决策树学习：决策树学习使用了一个决策树作为预测性模型，映射一个对象的观察结果给其目标价值一个推论。

关联规则学习:是一种用来在大型数据库中发现变量之间的有趣联系的方法,例如频繁模式挖掘。

人工神经网络：一个人工神经网络学习（ANN）算法，通常被称为神经网络（NN），是一个由生物的神经网络所激发出的一个算法。计算结构是由联结的人工神经元组所构成，通过联结式的方法来传递信息和计算。现代神经网络是非线性的统计学数据模型工具。它们通常被用来在输入和输出之间模拟复杂关系，找到数据中的关系，或者在观测变量中从不知道的节点捕获统计学结构。

深度学习：个人不能承受硬件的价格和GPU的发展推动了这些年深度学习的进步，深度学习是由人工神经网络中的多个隐藏层组成的。这条道路试图去模拟人脑的过程，光、声进入视觉和听觉。一些成功的应用有计算机视觉和演讲识别。

归纳逻辑编程：归纳逻辑编程（ILP）是一门用逻辑编程控制规则的学科，它使用统一的表示法来处理输入样例，背景知识和假说。给定已知的背景知识的编码和一组被表示为事实的逻辑数据库的示例，ILP系统将派生出一个假设的逻辑程序，该程序包含所有积极的和没有负面的示例。归纳编程是一个相关的领域，它考虑任何一种表示假设(而不仅仅是逻辑编程)的编程语言，例如函数式编程。

支持向量机：支持向量机是一系列关于监督学习在分类和回归上的应用。给出训练样本的数据集，每一个标记属于两类中的一类，一个SVM训练算法构成了一个模型，可以用来预测一个新的样本是否进入一个类别或者是另一个。

集群：集群分析是将一组观察结果分配到子集(称为集群)，这样，同一集群中的观察与一些预先确定的标准或标准相似，而来自不同集群的观察则不同。不同的聚类技术对数据的结构作出不同的假设，通常由一些相似性度量定义，并通过内部紧度(相同集群的成员之间的相似性)和不同的集群之间的分离来评估。其他方法基于估计的密度和图连通性。摘要聚类是一种非引导性学习的方法，是一种统计数据分析的常用技术。

贝叶斯网络：一个贝叶斯网络，信任网络或者有向无环图模型是一个概率性图的模型，它通过有向无环图代表了一系列的随机变量和他们的条件独立性。举例，一个贝叶斯网络代表着疾病和症状可能的关系。给出症状，网络可以被用来计算疾病出现的可能性。有效的算法存在于执行推理和学习的过程中。

增强学习：增强学习关心代理人如何在一个环境中采取行动，从而最大化一些长期受益的概念。增强学习算法尝试去寻找一些策略，映射当前世界的状态给代理在这些状态中应该采取的行动。

相似度量学习：在这个问题中，学习机被给予了很多对相似或者不相似的例子。它需要去学习一个相似的函数，以用来预测一个新的对象是否相似。它有时被用到推荐系统中。

遗传算法：遗传算法是一种启发式搜索，它模仿自然选择的过程，并且使用一些突变和变向来生成新的基因型，以找到好的情况解决问题。在机器学习中，遗传算法在20世纪80年代和90年代使用过。反之，机器学习技术被用来提高遗传和进化算法的表现。

基于规则的机器学习：基于规则的机器学习是任何机器学习方法的通用术语，它可以识别、学习或发展规则来存储、操作或应用知识。基于规则的机器学习者的定义特征是一组关系规则的标识和利用，这些规则集合了系统所捕获的知识。这与其他机器学习者形成鲜明对比，他们通常会识别出一种特殊的模型，这种模型可以普遍应用于任何实例，以便做出预测。基于规则的机器学习方法包括学习分类器系统、关联规则学习和人工免疫系统。

机器学习应用场景

活跃的领域：

• 数据分析
• 数据挖掘。
• 图像和语音识别
• 智能机器，机器人，人机对话，电脑博弈。

推荐系统：

• 基于物品的协同过滤
• 频繁模式挖掘

贝叶斯分类器：

• 垃圾邮件过滤
• 网页自动分类：自动化门户系统
• 评论自动分析

决策树

• 量化交易
• 智能博弈
• 局面标准化
• 局面评估函数
• 棋谱学习

神经网络和深度学习

• 语音识别,图像识别
• 图形识别：
• 车牌识别
• 指纹，虹膜纹识别
• 脸像识别
• 动态图像识别
• 小波分析

机器学习常用软件

常用软件列表：

• R（及其扩展包）
• Weka（Waikato Environment for Knowledge Analysis）
• Matlab
• Python,numpy,matplotlib,sklearn,tensorflow

代表性算法

回归预测及降维技术：

• 线性回归
• Logistic回归
• 主成分分析
• 因子分析
• 岭回归
• LASSO

分类器:

• 决策树
• 朴素贝叶斯
• 贝叶斯信念网络
• 支持向量机(SVM)
• 提升分类器准确率的Adaboost和随机森林算法

聚类和孤立点判别

• Kmeans聚类

人工神经网路及深度学习

• CNN
• RNN

…