EdmondFrank's 时光足迹

この先は暗い夜道だけかもしれない　それでも信じて進むんだ。星がその道を少しでも照らしてくれるのを。
或许前路永夜，即便如此我也要前进，因为星光即使微弱也会我为照亮前途。
——《四月は君の嘘》

Scala概率编程语言库-Figaro介绍

- -

Scala 的概率编程语言库-Figaro

什么是概率编程？

概率编程是一种系统创建方法，它所创建的系统能够帮助我们在面对不确定性时作出决策。

为什么使用概率编程？

概率推理是机器学习的基础技术之一。Google,Amazon和Microsoft等公司使用它理解可用数据。概率推理已经应用于各种各样的应用程序，如预测股价，推荐电影，诊断计算机和检测网络入侵。

  • 概率推理可用于预测未来，推断过去，以及从过去的事实中学习更好地预测未来。
  • 概率编程是使用图灵完备的编程语言作为表示语言的概率编程。

事实上：概率推理 + 图灵完备 = 概率编程

Figaro的简介

Figaro是一个内嵌于Scala编程语言的概率编程系统。除了继承了Scala的良好特性外，Figaro还提供了相当多的额外的优势，包括：

  • Figaro能够表示及其广泛的概率模型。Figaro元素的值可以为任何类型，包括布尔型，整数，双精度数，数组，树，图等。
  • Figaro提供了使用其条件和约束规定证据的丰富框架
  • Figaro有多种多样的推理算法
  • Figaro能够表示和推理随时间变化的的动态模型
  • Figaro能够在其模型中包含明确决策，并支持最优决策的推断。

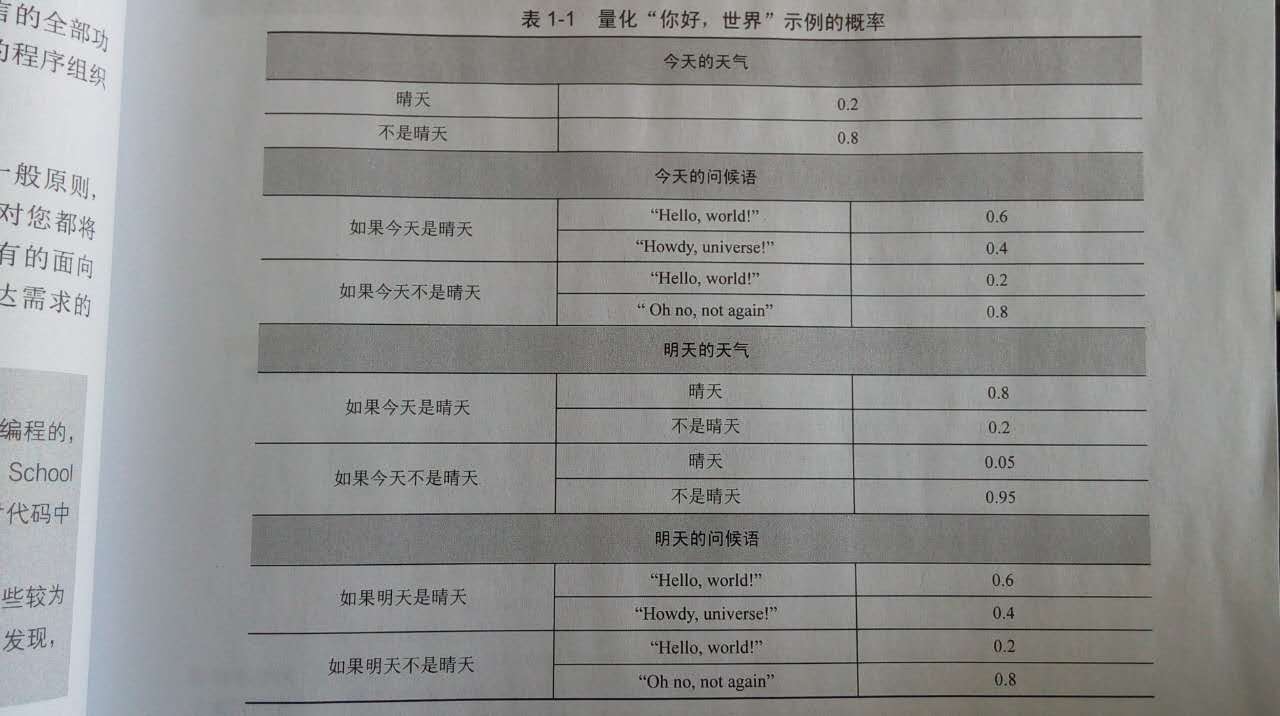
简单示例-量化“你好，世界”

图片截取自《概率编程实战》 表 1-1

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

mport com.cra.figaro.language._
import com.cra.figaro.library.compound.If
import com.cra.figaro.algorithm.factored.VariableElimination

object Main{
  val sunnyToday = Flip(0.2)
  val greetingToday = If(sunnyToday,
    Select(0.6 -> "Hello World",0.4 -> "Howdy universe"),
    Select(0.2 -> "Hello World",0.8-> "no not again!"))
  val sunnyTomorrow = If(sunnyToday, Flip (0.8) , Flip (0.05))
  val greetingTomorrow = If(sunnyTomorrow,
    Select(0.6 -> "Hello World",0.4 -> "Howdy universe"),
    Select(0.6 -> "Hello World",0.4 -> "no not again"))
  def predict: Unit ={
    val result = VariableElimination.probability(greetingToday,"Hello World")
    println("Today's greeting is \"Hello World!\" "+" with probability "+ result +".")
  }
  def infer: Unit = {
    val greeting = "Hello World"
    greetingToday.observe(greeting)
    val result = VariableElimination.probability(sunnyToday,true)
    println(s"If today's greeting is $greeting with probability $result.")
  }
  def learnAndPredict: Unit ={
    val greeting = "Hello World"
    greetingToday.observe(greeting)
    val result = VariableElimination.probability(greetingTomorrow,greeting)
    println(s"If today's greeting is $greeting,tomorrow's greeting will be $greeting\n" +
      s"with probability $result.")
  }


  def main(args: Array[String]): Unit = {
    predict
    infer
    learnAndPredict
  }

Python科学计算库NumPy的使用

- -

Python科学计算库NumPy的使用

NumPy的介绍

NumPy(Numerical Python的缩写)是一个开源的Python科学计算库。使用NumPy,就可以很自然地使用数组和矩阵。NumPy包含很多实用的数学函数,涵盖线性代数运算、傅里叶变换和随机数生成等功能。如果你的系统中已经装有LAPACK,NumPy的线性代数模块会调用它,否则NumPy将使用自己实现的库函数。LAPACK是一个著名的数值计算库,最初是用Fortran写成的,Matlab同样也需要调用它。从某种意义上讲,NumPy可以取代Matlab和Mathematica的部分功能,并且允许用户进行快速的交互式原型设计。

NumPy的数组对象

ndarray是一个多维数组对象，该对象由实际数据+描述性元数据组成。 使用Numpy需要先安装和导入NumPy库，有关安装教程可以参考Installing NumPy

导入语法：import numpy as np

此处使用np为别名是为了避免命名空间被污染。

特点：

  1. NumPy数组一般是同质（即数组内的元素为相同类型，特殊类型除外）
  2. NumPy数组的下标也是从0开始
  3. 可以方便地创建高维数组

eg：

1
2
3

In: a = np.arange(5)
In: a.dtype
Out: dtype('int64')

而在32位系统中，得到的结果类型可能是int32。

多维数组的创建：

1
2
3
4
5
6
7

In: m = np.array([np.arange(2), np.arange(2)])
In: m
Out:
array([[0, 1],
[0, 1]])
In: m.shape #shape可以输出数组行列（维度）信息
Out: (2, 2)

选取数组元素： 我们继续沿用上面创建的数组m

1
2
3
4

In: m[0,0]
Out: 0
In: m[0,1]
Out: 1

是的,从数组中选取元素就是这么简单。对于数组 a ,只需要用 a[m,n] 选取各数组元素,其中 m 和 n 为元素下标。

NumPy的数据类型: Python支持的数据类型有整型、浮点型以及复数型,但这些类型不足以满足科学计算的需求,因此NumPy添加了很多其他的数据类型。在NumPy中,许多函数的参数中可以指定数据类型,通常这个参数是可选的:

1
2

In: np.arange(7, dtype=uint16)
Out: array([0, 1, 2, 3, 4, 5, 6], dtype=uint16)

其中完整的数据类型可以通过np.sctypeDict.keys()查到：

1

dict_keys([0, 1, 2, 3, 'D', 5, 6, 'ushort', 8, 'P', 10, 11, 12, 'uintp', 14, 15, 16, 17, 18, 19, 'Float16', 21, 22, 23, 'cfloat', 4, 'Object0', 'int32', 'UInt64', 'Complex128', 'uint0', 'i2', 7, 'Int16', 'int', 'complex', 'ubyte', 'Int32', 'float', 'i', 'short', 'B', 'str0', 9, 'complex_', 'O', 'long', 'bytes', 'float_', 'Int64', 'int0', 'Void0', 'float128', 'Float64', 'Str0', 'int64', 'b', 'longdouble', 'void', 'f', 'longcomplex', 'ulonglong', 'intp', 'UInt32', 'V', 'object_', 'longlong', 'csingle', 'uint', 'c32', 'M', 'I', 'singlecomplex', 'double', 'timedelta64', 'object', 'unicode_', 'Float128', 'uint64', 'h', 'str', 'd', 'UInt8', 20, 'complex128', 'string_', 'clongfloat', 'H', 'm8', 'clongdouble', 'S', 'g', 'bool_', 'unicode', 'f16', 13, 'int8', 'void0', 'L', 'M8', 'uint32', 'p', 'bytes0', 'e', 'datetime64', 'U', 'float16', 'c16', '?', 'Bool', 'byte', 'i4', 'c8', 'int16', 'half', 'uint16', 'str_', 'i8', 'Complex32', 'Int8', 'bool', 'Bytes0', 'G', 'l', 'uint8', 'f2', 'single', 'f8', 'q', 'Q', 'm', 'Complex64', 'f4', 'u2', 'Float32', 'i1', 'u4', 'Datetime64', 'intc', 'float64', 'a', 'complex64', 'u1', 'bytes_', 'cdouble', 'object0', 'UInt16', 'bool8', 'float32', 'uintc', 'Timedelta64', 'F', 'longfloat', 'b1', 'u8', 'int_', 'complex256'])

创建自定义数据类型：

(1)创建数据类型

1
2
3

In: t = np.dtype([('name',np.str_,128),('count',np.int32),('price',np.float64)])
In: t
Out: dtype([('name', '<U128'), ('count', '<i4'), ('price', '<f8')])

(2)查看数据类型

1
2

In: t['name']
Out: dtype('<U128')

(3)使用自定义数据

1
2
3

In: itemz = np.array([('Meaning of life DVD', 42, 3.14), ('Butter', 13, 2.72)], dtype=t)
In: itemz[1]
Out: ('Butter', 13, 2.72)

一维数组的索引和切片：

1
2
3

In: a = np.arange(9)
In: a[3:7]
Out: array([3, 4, 5, 6])

多维数组索引和切片:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

In： b=np.arange(24).reshape(2,3,4)
In: b
Out: array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
In: b[0,2,1]
Out: 9-
#我们还可以这样写,选取第0组的所有元素:
In: b[0,:,:]
Out: array([[
0, 1, 2, 3],
[4, 5, 6, 7],
[8, 9,10,11]])

同时，b[0,:,:] == b[0,…]。 更多的多维数组的索引和切片操作可以参考NumPy使用手册

数组展平:

(1)ravel

1
2
3
4
5
6
7
8
9
10
11
12

In: b-
Out:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9,10,11]],
[[12,13,14,15],
[16,17,18,19],
[20,21,22,23]]])
In: b.ravel()
Out:
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])

(2)flatten

1
2
3
4

In: b.flatten()
Out:
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23])

flatten 和 ravel的区别在于：flatten函数会请求分配内存来保存结果，而reval函数只是返回数组的一个视图（view）

(3)改变数组的shape属性

1
2
3
4
5
6
7
8
9

In: b.shape = (6,4)
In: b
Out:
array([ 0, 1, 2, 3],
[ 4, 5, 6, 7],-
[ 8, 9,10,11],
[12,13,14,15],
[16,17,18,19],
[20,21,22,23]],

(4)transpose,相当与线性代数的转置

1
2
3
4
5
6

In: b.transpose()
Out:
array([[ 0, 4, 8,12,16,20],
[ 1, 5, 9,13,17,21],
[ 2, 6,10,14,18,22],
[ 3, 7,11,15,19,23]])

(5)resize，功能和reshape相同，但是resize会直接影响原操作数组

1
2
3
4
5

In: b.resize((2,12))
In: b
Out:
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[12,13,14,15,16,17,18,19,20,21, 22, 23]])

数组组合：

(1)水平组合

1
2
3
4
5
6

In: a = np.arange(9).reshape(3,3)
In: b=2*a
In: np.hstack((a,b))
Out: array([[ 0,  1,  2,  0,  2,  4],
       [ 3,  4,  5,  6,  8, 10],
       [ 6,  7,  8, 12, 14, 16]])

同样可以使用concatenate函数实现同样效果

1
2
3
4

In: concatenate((a,b),axis=1)
Out: array([[ 0, 1, 2, 0, 2, 4],
[ 3, 4, 5, 6, 8,10],
[ 6, 7, 8,12,14,16]])

(2)垂直组合

1
2
3
4
5
6
7

In: np.vsta-ck((a,b))
Out: array([[ 0,  1,  2],
   [ 3,  4,  5],
   [ 6,  7,  8],
   [ 0,  2,  4],
   [ 6,  8, 10],
   [12, 14, 16]])

同样可以使用concatenate函数实现同样效果

1
2
3
4
5
6
7
8

In: concatenate((a,b),axis=0)
Out: In: np.vstack((a,b))
Out: array([[ 0,  1,  2],
[ 3,  4,  5],
[ 6,  7,  8],
[ 0,  2,  4],
[ 6,  8, 10],
[12, 14, 16]])

(3)深度组合

深度组合,就是将一系列数组沿着纵轴(深度)方向进行层叠组合。举个例子,有若干张二维平面内的图像点阵数据,我们可以将这些图像数据沿纵轴方向层叠在一起,这就形象地解释了什么是深度组合。

1
2
3
4
5
6
7
8
9
10
11

In: np.dstack((a,b))
Out: array([[[ 0,  0],
        [ 1,  2],
        [ 2,  4]],
       [[ 3,  6],
        [ 4,  8],
        [ 5, 10]],

       [[ 6, 12],
        [ 7, 14],
        [ 8, 16]]])

(4)列组合,column_stack 函数对于一维数组将按列方向进行组合,而对于二维数组, column_stack 与 hstack 的效果是相同的

(5)行组合,当然,NumPy中也有按行方向进行组合的函数,它就是 row_stack 。对于两 个一维数组,将直接层叠起来组合成一个二维数组。同样，对于二维数组，row_stack 与 vstack 的效果是相同的。

数组分割:

NumPy数组可以进行水平、垂直或深度分割,相关的函数有 hsplit 、 vsplit 、 dsplit 和split 。我们可以将数组分割成相同大小的子数组,也可以指定原数组中需要分割的位置。

(1)水平分割

1
2
3
4
5
6
7
8
9
10
11
12

In: a
Out: array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
In: np.hsplit(a,3) #沿水平方向分割成三个大小相同的子数组
Out: [array([[0],
        [3],
        [6]]), array([[1],
        [4],
        [7]]), array([[2],
        [5],
        [8]])]

(2)垂直分割

1
2

In: np.vsplit(a,3) #在垂直方向上分割成三个大小相同的子数组
Out： [array([[0, 1, 2]]), array([[3, 4, 5]]), array([[6, 7, 8]])]

(3)深度分割,dsplit函数将按深度方向分割数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

In: np.dsplit(np.arange(27).reshape(3,3,3),3)
Out: [array([[[ 0],
         [ 3],
         [ 6]],

        [[ 9],
         [12],
         [15]],

        [[18],
         [21],
         [24]]]), array([[[ 1],
         [ 4],
         [ 7]],

        [[10],
         [13],
         [16]],

        [[19],
         [22],
         [25]]]), array([[[ 2],
         [ 5],
         [ 8]],

        [[11],
         [14],
         [17]],

        [[20],
         [23],
         [26]]])]

同时，hsplit,vsplit同样也可以用函数split来实现，其使用就像上面的数组组合函数concatenate类似

到此，NumPy的常规的数组操作基本就结束了！

有关统计学的一些笔记

- -

有关推断统计学

样本与总体

在统计中，一个总体包括事件的全部，而一个样本是总体的一小部分（子集） 。

推断统计学

推断统计学（Inferential statistics） 是使用样本归纳总体的一种统计方法。推断统计非常有用，因为他允许我们基于有限的信息（样本）对总体得出结论。

假设检验

当我们使用样本对总体进行推断时，这个过程为假设检验（Hypothesis testing）。在假设检验中，通常要陈述两个假设：原假设（null hypothesis） 和对立假设（alternative hypothesis）。原假设通常陈述处理没有效果，而对立假设陈述处理有效果。

单边检验和双边检验

在评估处理要看是否对任一方向有影响（了解得分是更高还是更低）时使用双边检验，而在母的仅仅是调查单一方向（仅仅是更高还是更低）时使用单边检验。

第一类错误和第二类错误

在假设检验中，使用样本对总体进行推断。因为样本是总体的不完整“图像”，所以在假设检验过程中，就可能有错误。有两类错误发生：第一类错误，第二类错误。如果在原假设是真实的情况下拒绝了原假设，就发生了第一类错误。如果在原假设是错误的情况下没有拒绝原假设，就发生了第二类错误。

功效

功效（power）等于原假设错误的拒绝原假设的概率（如果原假设是错误的，他也是被拒绝的，就是做了一个正确的决策）。功效的取值范围在0~1之间，数值越大，功效越大。

抽样误差

一般来说，样本越小，样本与总体的差异就越大。样本与总体的差异就是抽样误差（sampling error）

p-值

如果从总体中抽取的样本通常都是不相同的，那么我们应该如何确定样本之间存在有意义的差异，还是由于抽样误差所导致的结果。p-值表明在原假设为真时获得特定结果的的概率。在假设检验中，检验的p-值是和预先确定的数值进行比较的，且基于比较的结果，对原假设进行决策。在社会和行为科学中，常用0.05位水平，来评价p-值。

评价p-值过程如下： 1. 如果p-值小于或等于0.05（α），拒绝原假设（假定策略之间存在差异） 2. 如果p-值大于0.05（α），不能拒绝原假设（没有假定策略之间有差异）

效应量

效应量（effect sizes）一般用来描述策略组之间的差异程度，表明我们研究结果的大小。

贝叶斯算法在检测群聊垃圾广告中的应用

- -

贝叶斯算法在检测群聊垃圾广告中的应用

背景：

贝叶斯过滤器是一种基于统计学的过滤器方法，是建立在已有的统计结果之上的，所以在实现算法 之前需要先建立历史资料库，即，先提供两组已经标注好的训练数据。 在此附上训练数据链接：https://pan.baidu.com/s/1nuGW2Ul

基本原理：

当看到一段文本时，我们先假定它是广告文本的概率为50%，其实整个识别模式就像垃圾邮件过滤 一样，我们先用S来表示垃圾文本，用H来表示正常文本。因此，P(S)和 P(H)的先验概率都是 50%：

然后我们再对其进行分词解析处理，我们用W来表示其中存在的某个关键词，然后问题就转变成了在 某个词语W存在的情况之下，目标文本为垃圾文本的可能性有多大？而解决这个问题的关键就是计算 P（S|W）的值。根据条件概率公式我们可以写出以下等式。

公式之中，P(W|S)和P(W|H)分别代表在正常文本和垃圾文本之中，词语W出现的概率，而这个概率 我们可以根据已经标注的好训练数据中计算得出。这里，我们假设对于词语W来说，上面所提到的两个 概率分别为5%和0.05%，那么我们可以计算出P(S|W)＝ 99.0%

因此，根据我们得出的99%的后验概率，我们可以说词语W的推断能力很强，在垃圾文本和正常文本之 中有十分良好的推断效果。

联合概率计算

但是，一段文本中存在非常多的词汇，我们不能单凭一个单词就推断出这段文本的分类属性。因此， 常规的做法是我们需要选取出整段文本中，P(S|W)最高的15个词，然后计算它们的联合概率。 （其中可能存在的问题有：某些新词在历史数据中都不曾出现过，我们无法计算其P(S|W)的值， 对于这样的问题需要用到贝叶斯平滑的思想进行处理，本文为了从简，我们都先假设这类词的P(S|W) 值为0.4）

对于联合概率的补充解释：联合概率是指在多个事件发生的情况之下，另一个发生的概率有多大。 例如：已知，W1 和 W2为两个不同的词语，它们都出现在某段文本之中，那么这段文本为广告 文本的概率就是W1和W2的联合概率。

最后，根据提取的15个词，得出最终的概率计算公式

在得出最后的概率后，再对阈值（门槛值）进行比较，如：0.9,若 > 0.9 则15个词联合 认定为90%为垃圾文本！

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164

#encoding=utf-8
import re
import pickle
#spam类对象
import jieba;
import os;
class spamEmailBayes:
    #获得停用词表
    def getStopWords(self):
        stopList=[]
        for line in open("../data/stopwords"):
            stopList.append(line[:len(line)-1])
        return stopList;
    #获得词典
    def get_word_list(self,content,wordsList,stopList):
        #分词结果放入res_list
        res_list = list(jieba.cut(content))
        for i in res_list:
            if i not in stopList and i.strip()!='' and i!=None:
                if i not in wordsList:
                    wordsList.append(i)

    #若列表中的词已在词典中，则加1，否则添加进去
    def addToDict(self,wordsList,wordsDict):
        for item in wordsList:
            if item in wordsDict.keys():
                wordsDict[item]+=1
            else:
                wordsDict.setdefault(item,1)

    def get_File_List(self,filePath):
        filenames=os.listdir(filePath)
        return filenames

    #通过计算每个文件中p(s|w)来得到对分类影响最大的15个词
    def getTestWords(self,testDict,spamDict,normDict,normFilelen,spamFilelen):
        wordProbList={}
        for word,num  in testDict.items():
            if word in spamDict.keys() and word in normDict.keys():
                #该文件中包含词个数
                pw_s=spamDict[word]/spamFilelen
                pw_n=normDict[word]/normFilelen
                ps_w=pw_s/(pw_s+pw_n)
                wordProbList.setdefault(word,ps_w)
            if word in spamDict.keys() and word not in normDict.keys():
                pw_s=spamDict[word]/spamFilelen
                pw_n=0.01
                ps_w=pw_s/(pw_s+pw_n)
                wordProbList.setdefault(word,ps_w)
            if word not in spamDict.keys() and word in normDict.keys():
                pw_s=0.01
                pw_n=normDict[word]/normFilelen
                ps_w=pw_s/(pw_s+pw_n)
                wordProbList.setdefault(word,ps_w)
            if word not in spamDict.keys() and word not in normDict.keys():
                #若该词不在脏词词典中，概率设为0.4
                wordProbList.setdefault(word,0.4)
        sorted(wordProbList.items(),key=lambda d:d[1],reverse=True)[0:15]
        return (wordProbList)

    #计算贝叶斯概率
    def calBayes(self,wordList,spamdict,normdict):
        ps_w=1
        ps_n=1

        for word,prob in wordList.items() :
            print(word+"/"+str(prob))
            ps_w*=(prob)
            ps_n*=(1-prob)
        p=ps_w/(ps_w+ps_n)
#         print(str(ps_w)+"////"+str(ps_n))
        return p

    #计算预测结果正确率
    def calAccuracy(self,testResult):
        rightCount=0
        errorCount=0
        for name ,catagory in testResult.items():
            if (int(name)<1000 and catagory==0) or(int(name)>1000 and catagory==1):
                rightCount+=1
            else:
                errorCount+=1
        return rightCount/(rightCount+errorCount)

spam=spamEmailBayes()
#保存词频的词典
spamDict={}
normDict={}
testDict={}
#保存每封邮件中出现的词
wordsList=[]
wordsDict={}
#保存预测结果,key为文件名，值为预测类别
testResult={}
#分别获得正常邮件、垃圾邮件及测试文件名称列表
normFileList=spam.get_File_List("../data/normal")
spamFileList=spam.get_File_List("../data/spam")
testFileList=spam.get_File_List("../data/test2")
#获取训练集中正常邮件与垃圾邮件的数量
normFilelen=len(normFileList)
spamFilelen=len(spamFileList)
#获得停用词表，用于对停用词过滤
stopList=spam.getStopWords()
#获得正常邮件中的词频
for fileName in normFileList:
    wordsList.clear()
    for line in open("../data/normal/"+fileName,encoding='gbk'):
        #过滤掉非中文字符
        rule=re.compile(r"[^\u4e00-\u9fa5]")
        line=rule.sub("",line)
        #将每封邮件出现的词保存在wordsList中
        spam.get_word_list(line,wordsList,stopList)
    #统计每个词在所有邮件中出现的次数
    spam.addToDict(wordsList, wordsDict)
normDict=wordsDict.copy()

output = open('norm.pkl','wb')
pickle.dump(normDict,output,-1)
output.close()

#获得垃圾邮件中的词频
wordsDict.clear()
for fileName in spamFileList:
    wordsList.clear()
    for line in open("../data/spam/"+fileName,encoding='gbk'):
        rule=re.compile(r"[^\u4e00-\u9fa5]")
        line=rule.sub("",line)
        spam.get_word_list(line,wordsList,stopList)
    spam.addToDict(wordsList, wordsDict)
spamDict=wordsDict.copy()

output = open('spam.pkl','wb')
pickle.dump(spamDict,output,-1)
output.close()

output = open('model.pkl','wb')
pickle.dump(spam,output,-1)
output.close()

# 测试邮件
for fileName in testFileList:
    testDict.clear( )
    wordsDict.clear()
    wordsList.clear()
    for line in open("../data/test2/"+fileName):
    #for line in open("../data/test/"+fileName,encoding='gbk'):
        rule=re.compile(r"[^\u4e00-\u9fa5]")
        line=rule.sub("",line)
        spam.get_word_list(line,wordsList,stopList)
    spam.addToDict(wordsList, wordsDict)
    testDict=wordsDict.copy()
    #通过计算每个文件中p(s|w)来得到对分类影响最大的15个词
    wordProbList=spam.getTestWords(testDict, spamDict,normDict,normFilelen,spamFilelen)
    #对每封邮件得到的15个词计算贝叶斯概率
    p=spam.calBayes(wordProbList, spamDict, normDict)
    if(p>0.9):
        testResult.setdefault(fileName,1)
    else:
        testResult.setdefault(fileName,0)
#计算分类准确率（测试集中文件名低于1000的为正常邮件）
testAccuracy=spam.calAccuracy(testResult)
for i,ic in testResult.items():
    print(i+"/"+str(ic))
print(testAccuracy)