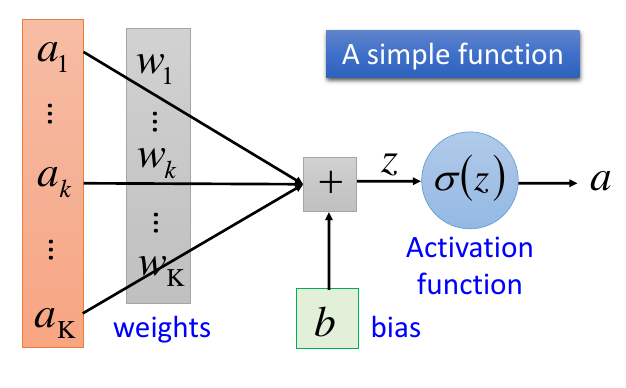
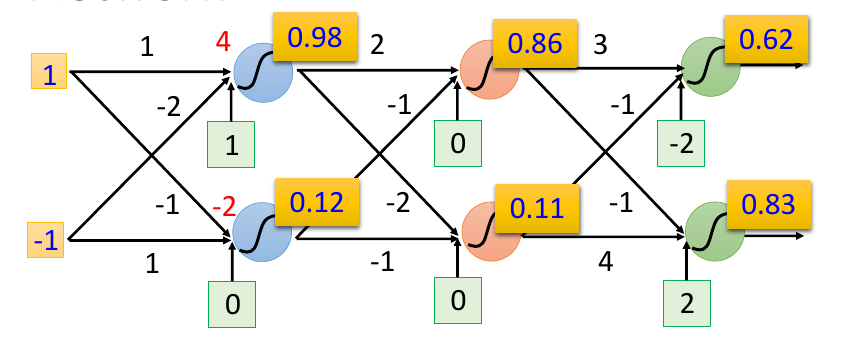
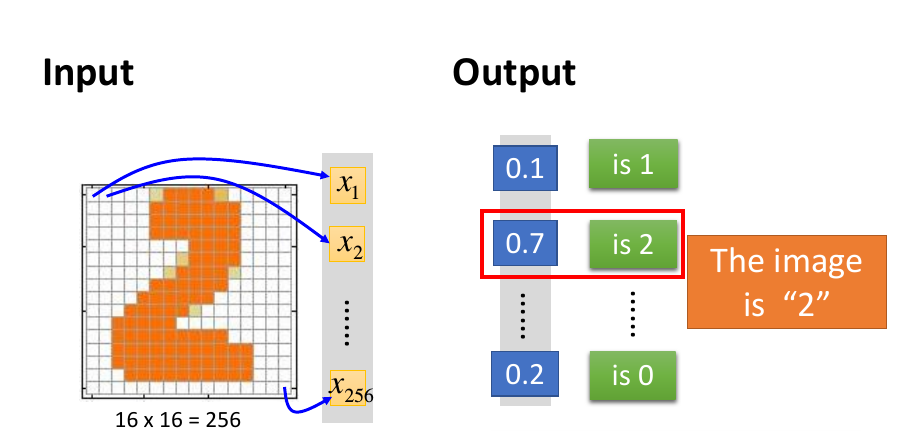
EM算法基石-最大似然估计

前言

在统计计算中，最大期望（EM）算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法（机器学习十大算法之一），其中概率模型依赖于无法观测的隐藏变量（Latent Variable）。最大期望经常用在机器学习和计算机视觉的数据聚类（Data Clustering）领域。而本文要讲的就是最大期望算法的基石-最大似然估计。

最大似然估计（Maximum Likelihood，ML）

概述

最大似然估计也称极大似然法，是一种统计方法，它用来求一个样本集的相关概率密度函数的参数。这个方法最早是遗传学家以及统计学家罗纳德·费雪爵士在1912年至1922年间开始使用的。

最大似然法明确地使用概率模型，其目标是寻找能够以较高概率产生观察数据的系统发生树。最大似然法是一类完全基于统计的系统发生树重建方法的代表。

简单举例

设有外形完全相同的两个箱子,甲箱有99个白球1个黑球,乙箱有1个白球99个黑球.今随机地抽取一箱,然后再从这箱中任取一球,结果发现是白球.问这个箱子是甲箱还是乙箱?

仅仅从取出的球是白球这一点是无法从逻辑上严格加以判定该箱究竟是甲箱还是乙箱的。但是如果现在一定要我们做出选择，那么我们只能这样来考虑：从箱中取出的球是白球这一点来看，甲箱和乙箱哪个看上去更像是真正从中取球的箱子？

我们可以这样来分析，如果该箱是甲箱,则取得白球的概率为0.99；如果该箱是乙箱,则取得白球的概率0.01．因此，用“该箱是甲箱”来解释所取的球是白球这一事件更有说服力一些，从而我们判定甲箱比乙箱更像一些。最后我们做出推断,这球是从甲箱取出的。

离散分布，离散有限参数空间

看完上面那个简单的例子，下面再来考虑一个抛硬币的例子。假设这个硬币正面跟反面轻重不同。我们把这个硬币抛80次，并把正面的次数记下来，正面记为H，反面记为T），并把抛出一个正面的概率记为p，抛出一个反面的概率记为1 − p。假设我们抛出了49个正面，31 个反面，即49次H，31次T。假设这个硬币是我们从一个装了三个硬币的盒子里头取出的。这三个硬币抛出正面的概率分别为p = 1 / 3, p = 1 / 2, p = 2 / 3. 这些硬币没有标记，所以我们无法知道哪个是哪个。使用最大似然估计，通过这些试验数据，我们可以计算出哪个硬币的可能性最大。这个可能性函数取以下三个值中的一个：

$$P(H=49,T=31|\rho=\frac{1}{3})=\textrm{C}^{49}_{80}(\frac{1}{3})^{49}(1-\frac{1}{3})^{31} \approx 0.000 \\ P(H=49,T=31|\rho=\frac{1}{2})=\textrm{C}^{49}_{80}(\frac{1}{2})^{49}(1-\frac{1}{2})^{31} \approx 0.012 \\ P(H=49,T=31|\rho=\frac{2}{3})=\textrm{C}^{49}_{80}(\frac{2}{3})^{49}(1-\frac{2}{3})^{31} \approx 0.054$$

我们可以看到当$\widehat{p}=2/3$时，可能性函数取得最大值。这就是p的最大似然估计。

离散分布，连续参数空间（升级版）

现在假设上面的例子中的盒子中有无数个硬币，对于$0\leq p \leq 1$中的任何一个p， 都有一个抛出正面概率为p的硬币对应，我们再来求其可能性函数的最大值：
$$f_D(H=49,T=31|\rho)=\textrm{C}^{49}_{80}\rho^{49}(1-\rho^{31})$$
两边同时取p微分
$$0=\rho^{48}(1-\rho)[49(1-\rho)-31\rho]$$
求得其解分别为：
$$\rho=0,\rho=1和\rho=\frac{49}{80}$$
使可能性最大的解显然是p = 49 / 80（因为p = 0 和p = 1 这两个解会使可能性为零）。因此我们说最大似然估计值为$\widehat{p}=49/80$.

这个结果很容易一般化。只需要用一个字母t代替49用以表达伯努利试验中的被观察数据（即样本）的成功次数，用另一个字母n代表伯努利试验的次数即可。使用完全同样的方法即可以得到最大似然估计值:
$$\widehat{p}=\frac{t}{n}$$

最大似然估计的一般求解步骤

1. 写出似然函数
   　　 $$L\theta=\prod_{i=1}^n p(x_i;\theta)(总体X为离散型时)\\ L\theta=\prod_{i=1}^n f(x_i;\theta)(总体X为连续型时)$$
   　　

2. 对似然函数两边取对数有
   $$lnL\theta=\sum_{i=1}^n lnp(x_i;\theta) \\ lnL\theta=\sum_{i=1}^n lnf(x_i;\theta)$$

3. 对lnL\theta求导数并令之为0：
   $$\frac{dlnL\theta}{d\theta}=0$$

此方程为对数似然方程。解对数似然方程所得，即为未知参数 的最大似然估计值。

举个栗子：连续分布，连续参数空间（终级版）

设总体 $X~N(μ，σ^2),μ，σ^2(正太分布)$为未知参数，$X1,X2...,Xn$是来自总体X的样本，$X1,X2...,Xn$是对应的样本值，求$μ与σ^2$的最大似然估计值。

解: X的概率密度为
$$f(x|μ，σ2)=\frac{1}{\sqrt{2\pi\sigma}}e^-\frac{(x_i-\mu)^2}{2\sigma^2} (-\infty<x<+\infty),$$
　　
可得似然函数如下：
$$L(μ，σ2)=\prod_{i=1}^n\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{(x_i-\mu)^2}{2{\sigma}^2}}$$

取对数，得

　　 $$lnL(μ，σ2)=-\frac{n}{2}ln(2\pi)-\frac{n}{2}ln(\sigma^2)-\frac{1}{2{\delta}^2}\sum_{i=1}^n{(x_i-\mu)}^2$$

令

$$\begin{cases}\frac{\partial}{\partial\mu}ln L(\mu,\sigma)=0,\\\frac{\partial}{\partial\sigma^2}\ln L(\mu,\sigma)=0,\end{cases}$$

可得

$$\begin{cases}\frac{1}{\sigma^2}(\sum_{i=1}^2x_i-n\mu)=0,\\-\frac{n}{2\sigma^2}+\frac{1}{2(\sigma^2)^2}\sum_{i=1}^n(x_i-\mu)^2=0.\end{cases}$$

解得

$$\begin{cases}\widehat{\mu}=\frac{1}{n}\sum_{i=1}^n x_i=\overline{x}, \\\widehat{\sigma}^2=\frac{1}{n}\sum_{i=1}^n(x_i-\overline{x})^2.\end{cases}$$

故$μ和δ2$的最大似然估计量分别为
$$\widehat{\mu}=\overline{X}，\widehat{\delta^2}=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^2$$



传统机器学习走向神经网络

神经网络的基本结构

首先我们先来看一下最基础的神经网络结构：

由上图的结构可以看出，这个神经网络具有三层，其中输入层不计。而中间的橙色层则为两层隐藏层，最右的蓝色层为输出层。输入从最左边的输入层进行输入，然后经过两次隐藏层和激活函数之后进行输出，这样我们可以把这个神经网络简单地表示成一下的式子：
$$Y_{out} = W_iX_{in}+B$$
W为X的权重，而B为函数的偏置。
其中，偏置值B的存在有利于打破数据对称的局面，使得神经网络可以应用在非对称的数据之上。

神经网络的基本算法

前向传导：前向传导的思想比较简单，下面的一张图足以概括它的主要思想。

反向传播：反向传播的方法其实也比较简单，其主要思想是涉及求偏导，以及链式求导法则。

梯度下降：梯度下降法是一个最优化算法，通常也称为最速下降法。最速下降法是求解无约束优化问题最简单和最古老的方法之一，虽然现已不具有实用性，但是许多有效算法都是以它为基础进行改进和修正而得到的。最速下降法是用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢。

朴素贝叶斯和神经网络

首先朴素贝叶斯算法的原始形式可以表达成以下的形式：
$G(x)=arg\ max\ p(y) \prod\limits^n_{i=1}p(x_i|y)^{x_i}$

除此之外，该算法还有一下特点：
$x_i只有0，1两种取值$
$x_i取1意味着x_i对应了的特征“出现了”$
$x_i取0意味着x_i对应了的特征“没出现”$

这样转换成矩阵的形式时，我们可以采用独热编码亦称One-hot Encode。
独热编码：

解决了分类标签的问题，那么我们又该怎样用神经网络的线性模型形式来表达贝叶斯公式中概率相乘的情况呢？

没错，就是使用对数函数。根据对数函数的性质$log_2X+log_2Y=log_2XY$,我们就可以通过对数变换，将乘法转换成加法的形式，我们可以把上面的朴素贝叶斯公式改写成：
$G(x)=arg\ max\ log(y)+\sum\limits^n_{i=1}x_ilog\ p(x_i|y)$

那么我们就可以用退化成线性模型的神经网络来实现朴素贝叶斯模型。

核心实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 独热化处理部分
from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder()
x_train = enc.fit_transform(x_train).toarray()
x_test = enc.transform(x_test).toarray()

## .....篇幅有限,此处省略其余代码

# NaiveBayes -> NN 权值转换部分
class NB2NN(TransformationBase):
    def __init__(self, *args, **kwargs):
        super(NB2NN, self).__init__(*args, **kwargs)
        self._name_appendix = "NaiveBayes"
        self.model_param_settings.setdefault("activations", None)

    def _transform(self):
        self.hidden_units = []
        x, y, x_test, y_test = self._get_all_data()
        nb = MultinomialNB()
        nb.fit(x, y)
        self._print_model_performance(nb, "Naive Bayes", x, y, x_test, y_test)
        self._transform_ws = [nb.feature_log_prob_.T]
        self._transform_bs = [nb.class_log_prior_]

决策树贝叶斯和神经网络

首先，决策树的原理主要就是通过数据信息熵的变化来选择当前的最优分类点，然后从根开始一步一步扩展成树。而实质上，最后成功构建出来的决策树，其从根节点开始到每个分类叶子节点的路径对应的都是一组高维空间上的超平面组合。决策树的分类也就是用一组超平面去划分数据空间，使得最后剩下一个唯一确定的标识。

知道决策树的本质之后，我们就可以用这样的方法来将决策树算法迁移到神经网络上：
* 第一个隐藏层表达决策树的中间节点所对应的超平面
* 第二个隐藏层表达各个决策的路径
* 第二个隐藏层和输出层之间的权值矩阵表达各个叶节点

核心实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87

## 因为决策树到神经网络的转换较为复杂,此处仅贴出核心代码
class DT2NN(TransformationBase):
    def __init__(self, *args, **kwargs):
        super(DT2NN, self).__init__(*args, **kwargs)
        self._name_appendix = "DTree"
        self.model_param_settings.setdefault("activations", ["sign", "one_hot"])

    def _transform(self):
        x, y, x_test, y_test = self._get_all_data()
        tree = DecisionTreeClassifier()
        tree.fit(x, y)
        self._print_model_performance(tree, "Decision Tree", x, y, x_test, y_test)

        tree_structure = export_structure(tree)
        n_leafs = sum([1 if pair[1] == -1 else 0 for pair in tree_structure])
        n_internals = n_leafs - 1

        print("Internals : {} ; Leafs : {}".format(n_internals, n_leafs))

        b = np.zeros(n_internals, dtype=np.float32)
        w1 = np.zeros([x.shape[1], n_internals], dtype=np.float32)
        w2 = np.zeros([n_internals, n_leafs], dtype=np.float32)
        w3 = np.zeros([n_leafs, self.n_class], dtype=np.float32)
        node_list = []
        node_sign_list = []
        node_id_cursor = leaf_id_cursor = 0
        max_route_length = 0
        self.hidden_units = [n_internals, n_leafs]

        for depth, feat_dim, rs in tree_structure:
            if feat_dim != -1:
                if depth == len(node_list):
                    node_sign_list.append(-1)
                    node_list.append([node_id_cursor, feat_dim, rs])
                    w1[feat_dim, node_id_cursor] = 1
                    b[node_id_cursor] = -rs
                    node_id_cursor += 1
                else:
                    node_list = node_list[:depth + 1]
                    node_sign_list = node_sign_list[:depth] + [1]
            else:
                valid_nodes = set()
                local_sign_list = node_sign_list[:]
                for i, ((node_id, node_dim, node_threshold), node_sign) in enumerate(
                    zip(node_list, node_sign_list)
                ):
                    valid_nodes.add((node_id, node_sign))
                    if i >= 1:
                        for j, ((local_id, local_dim, local_threshold), local_sign) in enumerate(zip(
                            node_list[:i], local_sign_list[:i]
                        )):
                            if node_sign == local_sign and node_dim == local_dim:
                                if (
                                    (node_sign == -1 and node_threshold < local_threshold) or
                                    (node_sign == 1 and node_threshold > local_threshold)
                                ):
                                    local_sign_list[j] = 0
                                    valid_nodes.remove((local_id, local_sign))
                                    break
                for node_id, node_sign in valid_nodes:
                    w2[node_id, leaf_id_cursor] = node_sign / len(valid_nodes)
                max_route_length = max(max_route_length, len(valid_nodes))
                w3[leaf_id_cursor] = rs / np.sum(rs)
                leaf_id_cursor += 1

        w2 *= max_route_length
        self._transform_ws = [w1, w2, w3]
        self._transform_bs = [b]

#................ 篇幅有限,省略其余代码

# DTree -> NN
def export_structure(tree):
    tree = tree.tree_

    def recurse(node, depth):
        feature_dim = tree.feature[node]
        if feature_dim == _tree.TREE_UNDEFINED:
            yield depth, -1, tree.value[node]
        else:
            threshold = tree.threshold[node]
            yield depth, feature_dim, threshold
            yield from recurse(tree.children_left[node], depth + 1)
            yield depth, feature_dim, threshold
            yield from recurse(tree.children_right[node], depth + 1)

    return list(recurse(0, 0))

模型改进

对于朴素贝叶斯

根据上述的原理和理论，我们可以将朴素贝叶斯和决策树转换成神经网络模型，但是转换之后是否存在意义呢？

首先本身可以通过简单log对数转换成线性模型的朴素贝叶斯算法来说，其转换的步骤并不复杂，但却能够对朴素贝叶斯的独立假设进行一定的微调修正。

对于决策树

那么对于决策树来说，神经网络的介入可以对决策树的硬边界作一定的修正和“软化”作用。



深度学习入门简介（二）

深度学习的三部曲

训练前的准备

1）训练数据
在训练一个深度学习的模型之前，我们首先需要准备的就是训练数据，若是图片的话其中就包括：图片的内容以及他的标签。
注：学习的分类目标也是包括在训练数据里面的

2）学习目标
学习的目标往往就是一个二分类或者多分类问题。而对于最后的效果，我们需要达到当我们输入一个待预测或分类的值时，正确的结果应该对应那个最大概率的输出项。

3）损失函数
简单来说，深度学习的分类和回归的本质就是，找到一个使得在所有样本项上取得的误差值最小的函数。而预测值与真实值的误差我们可以通过他们之间的距离计算得出。

最小化误差

为了达到一个分类或预测准确的效果，我们就要找到一个网络中的对应的超参数$\theta$使得网络的预测与真实值的误差是最小的。其中一个简单而粗暴的方法就是：枚举法。但是这样做的效率显然非常的低效。为了能够更加优化地找到或者说是接近使得网络取得最小误差的超参数$\theta$我们可以采用梯度下降法，其根据预设的学习率不断更新权重的梯度来接近局部最优解。

其具体过程图如下所示：

梯度下降的缺点：
由于梯度下降每次计算时都是随机选取一个开始点，再根据学习率来慢慢减小全局误差。这样一来，学习率的设定就十分重要了，过大的学习率容易越过最低点，而过小的学习率又使得误差降低的速度过慢，且过小的学习率也会造成学习过程中陷入局部最低点后无法跳出。但实际上由于精度误差的问题梯度下降永远无法到达真正意义上的全局最低点，即无法取得全局最有解。但在多次的迭代运算后一般可以达到一个可接受的损失误差的局部最优解。

具体图示如下：

反向传播

反向传播算法：这是一种高效的计算权值梯度的方式。

有关算法的详细介绍可以参考：

http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2015_2/Lecture/DNN%20backprop.ecm.mp4/index.html

通常我们在使用流行框架来构建神经网络时，不用亲自考虑如何去计算和处理梯度值，框架的作者在实现框架时已经做好了相关处理。

神经网络的理论

根据 A visual proof that neural nets can compute any function 文章的描述任何的连续函数 f 都可以用一个隐藏层内有足够多的神经元的神经网络来近似。

既然这样，为什么今天流行的是深度网络而不是广度网络呢？

根据 Seide, Frank, Gang Li, and Dong Yu. “Conversational Speech Transcription
Using Context-Dependent Deep Neural Networks.” Interspeech. 2011.
论文的研究，广度和深度网络对降低全局误差时的参数如下表所示：

根据上图的研究结果，我们可以发现使用多层的神经元能够更加容易近似一些函数，这其实就跟我们的电子电路中的逻辑电路类似，即便在电子电路中两层的逻辑门电路就可以实现任意的逻辑操作，但是使用多层的逻辑门电路可以更容易的构建一些逻辑操作。

模块化

深度学习中还有一个特点就是模块化，在一层层的网络层的堆叠中，每一层都会作为一个模块来学习数据。简单来说，深度学习的过程其实就是一个自动提取特征的过程。对于传统的机器学习而言，数据科学家通过特征工程，提取出数据的特征，再利用特征对数据进行建模以此达到分类预测的效果。深度学习通过各个神经元的加权组合以及反向传播的权值调整，使得整个网络的每一层都渐渐趋向稳定，且其稳定值能够在那个维度上进行部分数据的划分，简单来说就是一个区域性的能够对数据有所区分的特性。那随着各个神经层的共同作用使得深度学习在分类预测应用上效果显著。

最后，深度学习在图像分类的本质大概可以用以下这张图片概括：



深度学习入门简介

背景

深度学习的概念源于人工神经网络的研究。含多隐层的多层感知器就是一种深度学习结构。深度学习通过组合低层特征形成更加抽象的高层表示属性类别或特征，以发现数据的分布式特征表示。

概念

深度学习的概念由Hinton等人于2006年提出。基于深度置信网络(DBN)提出非监督贪心逐层训练算法，为解决深层结构相关的优化难题带来希望，随后提出多层自动编码器深层结构。此外Lecun等人提出的卷积神经网络是第一个真正多层结构学习算法，它利用空间相对关系减少参数数目以提高训练性能。

原理

深度学习是机器学习中一种基于对数据进行表征学习的方法。观测值（例如一幅图像）可以使用多种方式来表示，如每个像素强度值的向量，或者更抽象地表示成一系列边、特定形状的区域等。而使用某些特定的表示方法更容易从实例中学习任务（例如，人脸识别或面部表情识别）。深度学习的好处是用非监督式或半监督式的特征学习和分层特征提取高效算法来替代手工获取特征。

（以上内容摘取自百度百科）

个人理解：如果说机器学习是为了找出一个能够代表输入变量和输出变量的关系的函数的话；那么深度学习就是先根据输入和输出变量之间的关系，列出一系列能够代表他们之间关系的函数，然后再从这个函数集之中提取一个最优的函数。

结构

神经元

随着神经网络的应用和深度学习在人工智能领域的大放异彩，很多人都说神经网络的是最成功的仿真模型。那么他的结构究竟是怎样子的呢？

一个简单的神经网咯函数（一般称作：神经元），就如上图所示。

他的主要执行过程：

多个输入a X 各自的权重w + 偏置值b => 激活函数 => 输出

其中，在这个流程之中，我们可能比较迷惑的是那个激活函数Activation function。

Activation Function：即激活函数，目前的常用的激活函数由挺多的，例如，Simmoid Function，tanh，relu等等。虽然形式上不同，但是他们大体的目的都是较为一致的，就是用来加入非线性因素的，因为线性模型的表达能力不够。

$$如下所示的Sigmoid Function \\\sigma(z)=\frac{1}{1+e^{-z}}$$

同时，激活函数可以将非常大或非常小的数据映射到“逻辑空间”[-1,1]之间，这样映射过后的数据更适合在反向传播算法中进行梯度下降。

连接方式

上面我们提及的仅仅是神经网络中的一个神经元，他是神经网络之中最基本的组成单位。但是如果要构建一个强大智能的神经网络，仅仅靠一个神经元是不行的。于是，我们便可以将多个神经元分层连接起来，这样才构成了我们所知道的神经网络。

既然，神经网络的构成本质就是神经元的连接，那么不同的连接方式就会形成不同的神经网络结构如全连接前馈网络，多层感知器，卷积神经网络，循环神经网络等等。

全连接前馈网络

在众多的连接之间，全连接的前馈网络不仅较为简单，也是很多深层网络的基础。他的基本连接方式如下图片所示：

其中，一般来说神经网络的第一层通常都是输入层，而最后一层便是输出层以及中间的都统一称作隐藏层。深度神经网络中的“深”便代表了这个网络中间有非常多的隐藏层。

输出层

通常，输出层一般为Softmax 层，并且其可以为任意值。在应用中，输出的结果通常用概率的形式表达，其具体形式如下图所示：

那么，我们知道了神经网络的组成之后，我们要是想自己构建一个神经网络，我们又该如何确定神经网络的层数和每层的神经元的个数呢？

就目前来说，并没有相当的严谨的理论来指导神经网络的构建。我们往往需要依靠直觉和训练测试结果的误差反馈来一步一步选择我们的层数和神经元数以达到要求的效果。