Python在Spark上的机器学习之机器学习实战(下)
MLlib 的使用(续)
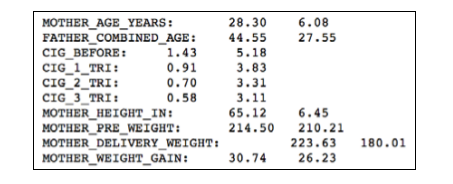
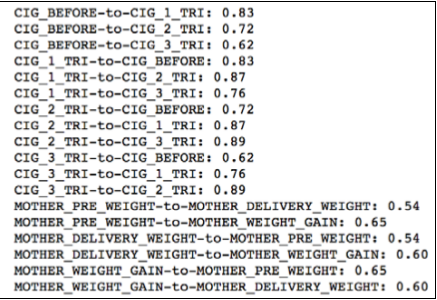
我们在上篇讲到了:数据相关性分析和特征选取,但是我们在上篇中所提及的方法基本都是针对标准的数值型的数据特征;那么,我们下篇就继续将分类变量的统计检验分析,以及最后的建模过程讲述完整。
统计校验
在通过特征变量的相关系数选择特征时,对于一般的分类变量而言,我们无法计算它们之间的相关系数,但是我们可以通过对它们进行卡方校验来检测它们的分布之间是否存在较大的差异。
卡方检验 :是用途非常广的一种假设检验方法,它在分类资料统计推断中的应用,包括:两个样本率或两个构成比比较的卡方检验;多个样本率或多个构成比比较的卡方检验以及分类资料的相关分析等。
卡方检验 就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,表明理论值完全符合。
而在PySpark中你可以用 .chiSqTest() 方法来轻松实现卡方检验。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import pyspark.mllib.linalg as ln
for cat in categorical_cols [ 1 :]:
agg = births_transformed \
. groupby ( 'INFANT_ALIVE_AT_REPORT' ) \
. pivot ( cat ) \
. count ()
agg_rdd = agg \
. rdd \
. map ( lambda row : ( row [ 1 :])) \
. flatMap ( lambda row :
[ 0 if e == None else e for e in row ]) \
. collect ()
row_length = len ( agg . collect ()[ 0 ]) - 1
agg = ln . Matrices . dense ( row_length , 2 , agg_rdd )
test = st . Statistics . chiSqTest ( agg )
print ( cat , round ( test . pValue , 4 ))
我们遍历所有的分类变量并以 infant_alive_ at_report 进行分类统计。下一步,我们需要将其转化成RDD,所以我们要先利用pyspark.mllib.linalg模将它们转换成一个矩阵。 .chiSqTest() 来校验我们的结果。
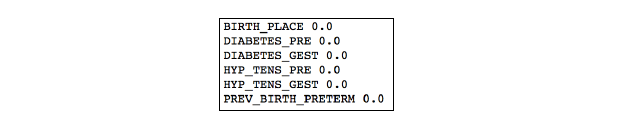
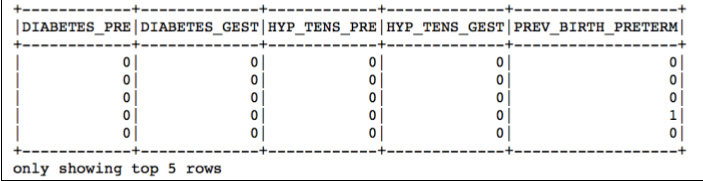
最后结果显示如下:
从结果我们可以看出,所有分类变量对理论值的预测都是有意义的,因此,我们在构建最后的预测模型的时候都要考虑上这些分类型特征变量。
创建最后的待训练数据集
经过一轮的数据分析和特征变量筛选之后,最终到了我们最终的建模阶段了。首先我们将筛选出来以DataFrame数据结构模型表达的数据转换成以LabeledPoints形式表示的RDD。
LabeledPoint 是 MLlib 中的一种数据结构,它包含了两个属性值:label(标识),features(特征)一般用作机器学习模型的训练。
其中,label就是我们目标的分类的标识而features就是我们用于分类的特征,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import pyspark.mllib.feature as ft
import pyspark.mllib.regression as reg
hashing = ft . HashingTF ( 7 )
births_hashed = births_transformed \
. rdd \
. map ( lambda row : [
list ( hashing . transform ( row [ 1 ]) . toArray ())
if col == 'BIRTH_PLACE'
else row [ i ]
for i , col
in enumerate ( features_to_keep )]) \
. map ( lambda row : [[ e ] if type ( e ) == int else e
for e in row ]) \
. map ( lambda row : [ item for sublist in row
for item in sublist ]) \
. map ( lambda row : reg . LabeledPoint (
row [ 0 ],
ln . Vectors . dense ( row [ 1 :]))
)
划分训练集和测试集
形如sklearn.model_selection.train_test_split随机划分训练集和测试集的模块一般,在PySpark中RDDs也有一个便利的.randomSplit(…) 方法用于随机划分训练集和测试集。
在本例中可以这样使用
births_train, births_test = births_hashed.randomSplit([0.6 , 0.4 ])没错,仅仅需要上面这样一行的代码,我们就可以将我们的待训练数据按照随机60%,40%来划分好我们的训练集和测试集了。
开始建模
在一切准备就绪之后,我们就可以开始通过我们上面的训练数据集来建模了。在这里我们来尝试建立两个模型:一个线性的Logistic回归模型,一个非线性的随机森林模型。然后,在初次建模的时候,我们先采用筛选出来的全部特征来建模,然后我们再通过ChiSqSelector(…) 方法来归纳出最能代表全部整体的四个主成分。
Logistic 回归模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from pyspark.mllib.classification \
import LogisticRegressionWithLBFGS
LR_Model = LogisticRegressionWithLBFGS \
. train ( births_train , iterations = 10 )
LR_results = (
births_test . map ( lambda row : row . label ) \
. zip ( LR_Model \
. predict ( births_test \
. map ( lambda row : row . features )))
) . map ( lambda row : ( row [ 0 ], row [ 1 ] * 1.0 ))
import pyspark.mllib.evaluation as ev
LR_evaluation = ev . BinaryClassificationMetrics ( LR_results )
print ( 'Area under PR: {0:.2f}' \
. format ( LR_evaluation . areaUnderPR ))
print ( 'Area under ROC: {0:.2f}' \
. format ( LR_evaluation . areaUnderROC ))
LR_evaluation . unpersist ()
从上面的建模过程可以看出,使用PySpark训练一个模型也是非常简单的。我们只需要调用.train(…) 方法,并传入之前处理好的LabeledPoints数据即可。不过需要注意的一点是我们要提前指定一个较小训练的迭代次数以免训练时间过长。
同时,在上面的代码中,我们在训练完一个模型之后使用MLlib中为我们提供的评估分类和回归准确度的.BinaryClassificationMetrics(…) 方法来分析我们最后预测的结果。
最后,结果图示如下:
通过PR,ROC的结果,我们可以看出,这个模型还是可接受的。
选取出最具代表性的分类特征
通常来说,一个采取更少的特征的简单模型,往往会比一个复杂的模型,在分类问题上更具有代表性和可解释性。而在MLlib中,则可以通过.Chi-Square selector 来提取出模型中最具代表性的一些分类特征变量来简化我们的模型。
1
2
3
4
5
6
7
8
9
10
11
12
13
selector = ft . ChiSqSelector ( 4 ) . fit ( births_train )
topFeatures_train = (
births_train . map ( lambda row : row . label ) \
. zip ( selector \
. transform ( births_train \
. map ( lambda row : row . features )))
) . map ( lambda row : reg . LabeledPoint ( row [ 0 ], row [ 1 ]))
topFeatures_test = (
births_test . map ( lambda row : row . label ) \
. zip ( selector \
. transform ( births_test \
. map ( lambda row : row . features )))
) . map ( lambda row : reg . LabeledPoint ( row [ 0 ], row [ 1 ]))
随机森林模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from pyspark.mllib.tree import RandomForest
RF_model = RandomForest \
. trainClassifier ( data = topFeatures_train ,
numClasses = 2 ,
categoricalFeaturesInfo = {},
numTrees = 6 ,
featureSubsetStrategy = 'all' ,
seed = 666 )
RF_results = (
topFeatures_test . map ( lambda row : row . label ) \
. zip ( RF_model \
. predict ( topFeatures_test \
. map ( lambda row : row . features )))
)
RF_evaluation = ev . BinaryClassificationMetrics ( RF_results )
print ( 'Area under PR: {0:.2f}' \
. format ( RF_evaluation . areaUnderPR ))
print ( 'Area under ROC: {0:.2f}' \
. format ( RF_evaluation . areaUnderROC ))
model_evaluation . unpersist ()
随机森林模型(Random forest 后面简称RF)在训练上总体与Logistic类似,不同的参数是RF在训练前需要指定类别总数:numClasses,树的棵数:numTrees(这两个参数的意义大家可以参照下随机森林模型的百科介绍 )
注:在随机森林模型的创建中,我们采用的是上面提取出来的最具代表性的有效特征,这就意味着模型用到的特征是比之前的Logistic要少的。
最后,结果图示如下:
通过结果我们可以看出,随机森林模型,在采用比之前更少的特征下的建模的最终预测效果是由于之前的Logistic回归模型的。
下面我们同样使用代表性特征来重建一次Logistic回归模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
LR_Model_2 = LogisticRegressionWithLBFGS \
. train ( topFeatures_train , iterations = 10 )
LR_results_2 = (
topFeatures_test . map ( lambda row : row . label ) \
. zip ( LR_Model_2 \
. predict ( topFeatures_test \
. map ( lambda row : row . features )))
) . map ( lambda row : ( row [ 0 ], row [ 1 ] * 1.0 ))
LR_evaluation_2 = ev . BinaryClassificationMetrics ( LR_results_2 )
print ( 'Area under PR: {0:.2f}' \
. format ( LR_evaluation_2 . areaUnderPR ))
print ( 'Area under ROC: {0:.2f}' \
. format ( LR_evaluation_2 . areaUnderROC ))
LR_evaluation_2 . unpersist ()
最终结果:
通过结果,我们可以看出,虽然没有达到RF模型的准确度,但是与采用了全特征的Logistic回归模型处于同一水平。所以,我们在可选的情况下,通常采用更少的特征来构建更为简化和有效的模型。
小结
到这里,Python在Spark上的机器学习的实战案例也结束了,欢迎大家继续关注我的博客。